1 Hamiltonian systems and Modeling of Mechanical sys- tems
This project is taken from [NSS14, chapter 5, D Project]. The problems in this project explore the Hamiltonian formulation of the laws of motion of a system and its phase plane implications. This formulation replaces Newton’s second law F = ma = my” and is based on three mathematical manipulations:
• 
It is presumed that the force F (t, y, yj) depends only on y and 
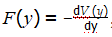, where V(y)
is called the potential.
• The velocity variable y’ is replaced throughout by the momentum yj = p/m.
• The Hamiltonian of a system (conservative or not) is defined as
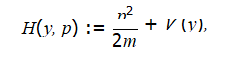
i.e. the sum of the kinetic and potential energy.
With these in mind we express the equation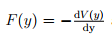
as the following system called Hamilton’s equations:
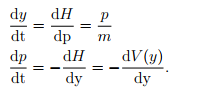
These equations imply by chain rule that
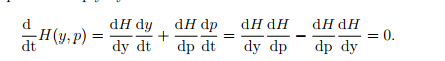
Therefore, the Hamiltonian remains constant along solution curves γ(t) = (y(t), p(t)) of the above system. This is the equivalent formulation of the conservation of energy when the forces are conservative (i.e. do not change in time such as gravity).
Hamilton’s formulation for mechanical systems and the conservation of energy principle imply that the phase plane trajectories of conservative systems lie on the curves where the Hamiltonian H1y, p2 is constant, and plotting these curves may be considerably easier than solving for the trajectories directly (which, in turn, is easier than solving the original system!).
A general system
has a Hamiltonian function H if
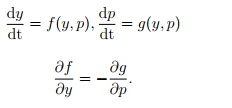
Because then if we define H by
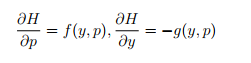
then we have conservation of energy:
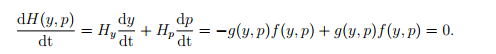
Project "Hamiltonian systems and Modeling of Mechan- ical systems" Problems
1. (30 points) For the mass–spring oscillator the spring force is given by F (y) = k y(where k is the spring constant).
(a) (5 points) For a general Hamiltonian system
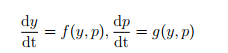
compute its linearization and plug in the Hamiltonian equations to conclude that a Hamiltonian system cannot have spiral sinks or sources critical point\-s.
(b) (5 points) Show that the above system with spring force F (y) = k y is Hamiltonian and then find the Hamiltonian and express Hamilton’s equations.
(c) (10 points)As done for autonomous systems, take the ratio of the equations and show that the phase plane trajectories H(y, p) = constant for this system are the ellipses given by p2/2m + ky2/2 = constant.
(d) (10 points)Bonus: Plot the direction field and some of the ODE solutions using an ODE solver.
(e) (10 points) Linearize the system on the critical point\-s and deduce the stability behaviour. Does that agree with part 1? Does it agree with the direction field (if you did the matlab part)?
2. (70 points) Stability and damping.
The damping force -by’ considered is not conservative, of course. Physically speaking, we know that damping drains the energy from a system until it grinds to a halt at an equilibrium point. In the phase plane, we can qualitatively describe the trajectory as continuously migrating to successively lower constant-energy orbits; stable centers become asymptotically stable spiral points when damping is taken into consideration. The second Hamiltonian equation, which effectively states pj = myjj = F , has to be changed to
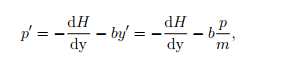
when damping is present.
Periodic force: For a pendulum system with a periodic force given by
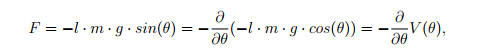
where l is the length of the pendulum. With damping present and using that the angular momentum is p = ml2θj, the Hamiltonian equations are:
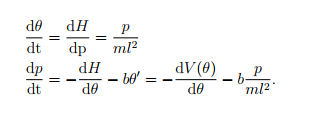
(a) (5 points) Derive the Hamiltonian for the undamped system (b=0) and sketch the phase trajectories.
(b) (5 points) Bonus: Plot the Hamiltonian trajectories using software.
(c) (10 points) Obtain the linearization for the undamped system and the damped system around arbitrary point.
(d) (30 points) Linearize the undamped system around each of the critical point\-s and based on the eigenvalues identify the qualitative behaviour (saddle-unstable, unstable or stable node).
(e) (5 points) Bonus: Plot the direction field and the ODE solutions using an ODE solver. Compare them to those of the Hamiltonian.
(f) (30 points) Linearize the damped system around each of the critical point\-s and based on the eigenvalues identify the qualitative behaviour (saddle-unstable, unstable or stable node). What happens to the stability behaviour as the damping b gets smaller?
(g) (5 points) Bonus: Plot the direction field and the ODE solutions using an ODE solver. Compare them to those of the Hamiltonian as the damping b gets smaller.
References
[NSS14] R Kent Nagle, Edward B Saff, and Arthur David Snider. Fundamentals of differential equations. Pearson Education, 2014.
代写CS&Finance|建模|代码|系统|报告|考试
编程类：C代写,JAVA代写 ,数据库代写,WEB代写,Python代写,Matlab代写,GO语言,R代写
金融类：统计，计量，风险投资，金融工程，R语言，Python语言，Matlab，建立模型，数据分析，数据处理
服务类：Lab/Assignment/Project/Course/Qzui/Midterm/Final/Exam/Test帮助代写代考辅导
天才写手,代写CS,代写finance,代写statistics,考试助攻
E-mail:850190831@qq.com 微信：BadGeniuscs 工作时间：无休息工作日-早上8点到凌晨3点
如果您用的手机请先保存二维码到手机里面，识别图中二维码。如果用电脑，直接掏出手机果断扫描。
