Subject of Economics
Degree of MSc Resit Degree Exam
Basic Econometrics, ECON5002
Wednesday, 02 August 2017,14:30 – 16:30
Instructions to students:
· No candidate will be permitted to leave within the first hour or the last half hour of this exam.
· Both entry and exit to the examination hall shall be at the absolute discretion of the invigilator.
· Students should answer ONE question from Section A and ONE question from Section B.
Materials supplied:
· Tables: Table D.2 – Percentage Points of t Distribution on Final Page
Materials allowed:
· Calculators:
o You may use Business School approved models only: Casio FX-83GT/Casio-83GT+, Casio FX-85GT/Casio FX-85GT+, Sharp EL531WH, Aurora AX-582BL.
· Students are entitled to use a single A4 double-sided sheet of pre-written notes
Using exam answer sheets
· Always use a black pen.
· Complete personal information on all white sheets supplied before the exam begins.
· Write your answer to each question on a SEPARATE white answer sheet, using BOTH sides if required. For this exam, the required number of white answer sheets is 2.
· Request yellow continuation sheets to continue an answer if one white sheet is not enough.
· Use the standard character set, printed below, when hand writing in data boxes. E.g. Student ID, Date of Birth, Question Number. Keep your characters inside the boxes.
· You must return all white answer sheets to the invigilator even if you have not attempted all questions.
This page has been left blank for student notes – anything written here will not be marked.
Section A
You must answer one question from this section.
You must use ONE WHITE answer sheet per question. To provide an answer that exceeds the space on the answer sheet, please raise your hand to request a YELLOW answer sheet.
1. Consider the simple regression with a constant
Yi = α + βXi + ui, i = 1, . . . , n. (1)
1.1. Verify the following numerical properties for the OLS estimator:
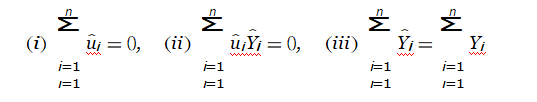
where uˆi = Yi − Yˆi, Yˆi = αˆ + βˆXi, and αˆ and βˆ denote the OLS
estimators of α and β, respectively. [20%]
1.2. Set β = 0 in model (1), that is, consider the model
Yi = α + ui, i = 1, . . . , n. (2)
Assume that ui i.i.d.(0, σ2), that is, the errors ui are independent and identically distributed across i, with mean zero and variance σ2.
Show that the OLS estimator of α, αˆ, is equal to Y¯ = n−1 Σn Yi
and the variance of αˆ is σ2/n. [20%]
1.3. Verify which of the numerical properties described in sub-question
1.1. hold for the OLS estimator of model (2). [10%]
2. Let F (FEMALE) be a variable which takes the value “0” for male and “1” for female. Similarly, the variable M (MALE) takes on the value “1” for male and “0” for female. Y denotes the Earnings.
For a given parameter θ, let θˆ denote its OLS estimator.
2.1. Derive the OLS estimators of αF and αM for the regression model
Yi = αF Fi + αM Mi + ui, i = 1, . . . , n (3) Show that αˆF = Y¯F , the average of the Yi’s only for females, and
αˆM = Y¯M , the average of the Yi’s only for males. [20%]
Continued overleaf
2.2. Consider the regression
Yi = α + βFi + ui, i = 1, . . . , n. (4) Substitute M = 1 − F in (3) and show that α = αM and β =
αF − αM . [10%]
2.3. Derive the OLS estimators of α and β for model (4). Show that αˆ = αˆM and βˆ = αˆF αˆM , where αˆF and αˆM have been derived in sub-question 2.1. [20%]
Section B
You must answer one question from this section.
You must use ONE WHITE answer sheet per question. To provide an answer that exceeds the space on the answer sheet, please raise your hand to request a YELLOW answer sheet.
3. Consider the following wage-determination equation for the British econ- omy for the period 1950-1969:
Wt = 8.582 + 0.364 P Ft + 0.004 P Ft−1 2.560 Ut
(1.129) (0.080) (0.072) (0.658)
(5)
where
W= wages and salaries per employee. PF= prices of final output at factor cost.
U= unemployment in Great Britain as a percentage of the total number of employees in Great Britain.
t= time, measured in years.
The figures in parenthesis are standard errors. The R2 of the regression is 0.873.
3.1. Interpret briefly the preceding equation. [12.5%]
3.2. What is the rationale for the introduction of P Ft−1?. [12.5%]
Continued overleaf
3.3. Should the variable P Ft−1 be dropped from the model? Explain
your answer. [12.5%]
3.4. Suppose that you are asked to estimate the elasticity of wages and salaries per employee with respect to the price of final output. How would you modify the regression model (5) to accomplish your task? [12.5%]
4. Consider the Cobb-Douglas production function
Y = β1Lβ2 Kβ3 (6)
where Y = output, L = labour input, and K = capital input.
Dividing equation (6) through by K, we get
(Y /K) = β1 (L/K)β2 Kβ2+β3−1 (7)
Taking the natural log of (7) and adding the error term, we obtain
ln (Y /K) = β0 + β2 ln (L/K) + (β2 + β3 − 1) ln (K) + u (8) where β0 = ln(β1).
4.1. Suppose you had data to run the regression (8). How would you test the hypothesis that there are constant returns to scale, that is, (β2 + β3) = 1? [17%]
4.2. If there are constant returns to scale, how would you interpret re- gression (8)? [16%]
4.3. Suppose we divide (6) by L rather than by K. Assuming constant returns to scale, how would you interpret this regression? [17%]
END OF QUESTION PAPER
APPENDIX D: STATISTICAL TABLES 961
TABLE D.2 PERCENTAGE POINTS OF THE t DISTRIBUTION
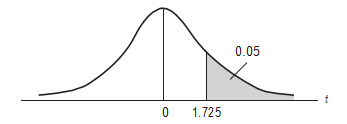Example
Pr (t > 2.086) = 0.025
Pr (t > 1.725) = 0.05 for df = 20
Pr (|t | > 1.725) = 0.10
t
0 1.725
|
Pr df |
0.25 0.50 |
0.10 0.20 |
0.05 0.10 |
0.025 0.05 |
0.01 0.02 |
0.005 0.010 |
0.001 0.002 |
|
1 |
1.000 |
3.078 |
6.314 |
12.706 |
31.821 |
63.657 |
318.31 |
|
2 |
0.816 |
1.886 |
2.920 |
4.303 |
6.965 |
9.925 |
22.327 |
|
3 |
0.765 |
1.638 |
2.353 |
3.182 |
4.541 |
5.841 |
10.214 |
|
4 |
0.741 |
1.533 |
2.132 |
2.776 |
3.747 |
4.604 |
7.173 |
|
5 |
0.727 |
1.476 |
2.015 |
2.571 |
3.365 |
4.032 |
5.893 |
|
6 |
0.718 |
1.440 |
1.943 |
2.447 |
3.143 |
3.707 |
5.208 |
|
7 |
0.711 |
1.415 |
1.895 |
2.365 |
2.998 |
3.499 |
4.785 |
|
8 |
0.706 |
1.397 |
1.860 |
2.306 |
2.896 |
3.355 |
4.501 |
|
9 |
0.703 |
1.383 |
1.833 |
2.262 |
2.821 |
3.250 |
4.297 |
|
10 |
0.700 |
1.372 |
1.812 |
2.228 |
2.764 |
3.169 |
4.144 |
|
11 |
0.697 |
1.363 |
1.796 |
2.201 |
2.718 |
3.106 |
4.025 |
|
12 |
0.695 |
1.356 |
1.782 |
2.179 |
2.681 |
3.055 |
3.930 |
|
13 |
0.694 |
1.350 |
1.771 |
2.160 |
2.650 |
3.012 |
3.852 |
|
14 |
0.692 |
1.345 |
1.761 |
2.145 |
2.624 |
2.977 |
3.787 |
|
15 |
0.691 |
1.341 |
1.753 |
2.131 |
2.602 |
2.947 |
3.733 |
|
16 |
0.690 |
1.337 |
1.746 |
2.120 |
2.583 |
2.921 |
3.686 |
|
17 |
0.689 |
1.333 |
1.740 |
2.110 |
2.567 |
2.898 |
3.646 |
|
18 |
0.688 |
1.330 |
1.734 |
2.101 |
2.552 |
2.878 |
3.610 |
|
19 |
0.688 |
1.328 |
1.729 |
2.093 |
2.539 |
2.861 |
3.579 |
|
20 |
0.687 |
1.325 |
1.725 |
2.086 |
2.528 |
2.845 |
3.552 |
|
21 |
0.686 |
1.323 |
1.721 |
2.080 |
2.518 |
2.831 |
3.527 |
|
22 |
0.686 |
1.321 |
1.717 |
2.074 |
2.508 |
2.819 |
3.505 |
|
23 |
0.685 |
1.319 |
1.714 |
2.069 |
2.500 |
2.807 |
3.485 |
|
24 |
0.685 |
1.318 |
1.711 |
2.064 |
2.492 |
2.797 |
3.467 |
|
25 |
0.684 |
1.316 |
1.708 |
2.060 |
2.485 |
2.787 |
3.450 |
|
26 |
0.684 |
1.315 |
1.706 |
2.056 |
2.479 |
2.779 |
3.435 |
|
27 |
0.684 |
1.314 |
1.703 |
2.052 |
2.473 |
2.771 |
3.421 |
|
28 |
0.683 |
1.313 |
1.701 |
2.048 |
2.467 |
2.763 |
3.408 |
|
29 |
0.683 |
1.311 |
1.699 |
2.045 |
2.462 |
2.756 |
3.396 |
|
30 |
0.683 |
1.310 |
1.697 |
2.042 |
2.457 |
2.750 |
3.385 |
|
40 |
0.681 |
1.303 |
1.684 |
2.021 |
2.423 |
2.704 |
3.307 |
|
60 |
0.679 |
1.296 |
1.671 |
2.000 |
2.390 |
2.660 |
3.232 |
|
120 |
0.677 |
1.289 |
1.658 |
1.980 |
2.358 |
2.617 |
3.160 |
|
∞ |
0.674 |
1.282 |
1.645 |
1.960 |
2.326 |
2.576 |
3.090 |
Note: The smaller probability shown at the head of each column is the area in one tail; the larger probability is the area in both tails.
Source: From E. S. Pearson and H. O. Hartley, eds., Biometrika Tables for Statisticians, vol. 1, 3d ed., table 12, Cambridge University Press, New York, 1966. Reproduced by permission of the editors and trustees of Biometrika.
Before your exam answers are collected:
Please ensure that you have written the course code (on the front of this exam paper), your student ID, date of birth and the number of the question that you have attempted on each answer sheet.
Put your exam answers in the order of the question number, ensuring that yellow answer sheets follow the appropriate white answer sheet.
Do not place any other exam materials, including the exam paper, beside the A3 answer sheets.
代写CS&Finance|建模|代码|系统|报告|考试
编程类：C代写,JAVA代写 ,数据库代写,WEB代写,Python代写,Matlab代写,GO语言,R代写
金融类：统计，计量，风险投资，金融工程，R语言，Python语言，Matlab，建立模型，数据分析，数据处理
服务类：Lab/Assignment/Project/Course/Qzui/Midterm/Final/Exam/Test帮助代写代考辅导
天才写手,代写CS,代写finance,代写statistics,考试助攻
E-mail:850190831@qq.com 微信：BadGeniuscs 工作时间：无休息工作日-早上8点到凌晨3点
如果您用的手机请先保存二维码到手机里面，识别图中二维码。如果用电脑，直接掏出手机果断扫描。
