MT4515 Functional Analysis – Class Test 2
Functional Analysis代写 Show that (T fn) is an equicontinuous family of functions. Why does (T fn) have a convergentsubsequence?
Answer all three questions. You should fully justify your answers which should be presented clearly and logically. Standard theorems may be used provided their use is clearly indicated.
Q1. As usual, C[0, 1] denotes the space of continuous real valued functions on [0, 1] and the supremum norm || || ∞ is given by || f|| ∞ = supt∈[0,1] |f(t)|. Functional Analysis代写
Let T : (C[0, 1], || || ∞) → (C[0, 1], || || ∞) be the linear operator defifined by
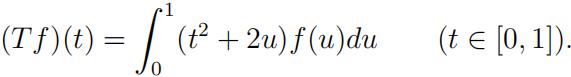
(a) Show that T is bounded and fifind the induced norm ||T|| of T.
(b) Let (fn) ∈ C[0, 1] be a sequence of functions such that ||fn|| ∞ ≤ 1 for all n ∈ N. Show that (T fn) is an equicontinuous family of functions. Why does (T fn) have a convergentsubsequence?6 marks

Q2. Recall that l 1 is the (real) normed space of real sequences Functional Analysis代写
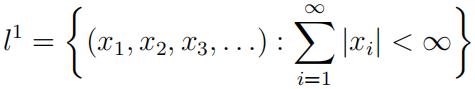
which is complete under the norm
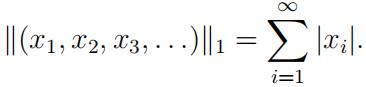
Let U : l 1 → l 1 be the linear operator given by
U(x1, x2, x3, . . .) = (2x2, 2x3, 2x4, . . .). Functional Analysis代写
(a) Show that U is bounded and fifind the induced norm ||U|| of U.
(b) Find the eigenvalues and corresponding eigenvectors of U. Hence fifind the spectrum σ (U) of U.6 marks
Q3. Let (X.〈 . 〉) be a real inner product space and let Y be a vector subspace of X. Let x ∈ X. Show that if y ∈ Y is such that ||x- y|| takes its minimum value (i.||x – y|| = infz∈y ||x -z|| then (x – y,w) = 0 for all w ∈ Y.
Hint: consider (x – y – λw, x – y – λw) for > λ R.

