PHYC30018 ASSIGNMENT for 2023
量子物理作业代写 For uncoupled oscillators, use separated-variables functions of the form f(x1)g(x2) to solve the energy eigenvalue problem.
Worth 15% of your fifinal mark. Due Thursday 30 March before 5pm.
Please submit your assignment through LMS.
You are not permitted to use ChatGPT or any other AI tool to complete this assignment. You must show all lines of algebra. You are permitted to discuss the assignment questions with other stu-dents, but if you do so then write down the names of those students in your submitted work.
Question 1 量子物理作业代写
(a) Use the standard Gaussian integral formula
![]()
where a > 0 and b may be complex, to prove in two complementary ways that
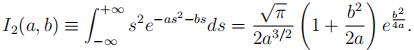
The two complementary ways are:
(i) By difffferentiating I0 twice with respect to b.
(ii) By difffferentiating I0 with respect to a.
(b) The wave function for a particle travelling in 1-dimension is
ψ(x) = Nx2 e−αx2
where α > 0 and N is a normalisation constant.
(i) Work out what N has to be for ψ(x) to be conventionally normalised.
(ii) Compute the momentum-space wave function φ(p) corresponding to ψ(x). 量子物理作业代写
(c) It can be shown that Gaussian integrals where a is a complex number such that Re(a) ≥ 0 are also well-defifined. They are called Fresnel integrals. (A famous example is R ![]() with a a real number.)
with a a real number.)
Now, suppose that the ψ(x) in (b) above is the wave function for a free particle at an initial time t = 0.
Explain how you would go about computing the time-evolved coordinate-space wave function ψ(x, t) through use of the momentum-space wave func-tion φ(p) you computed in (b)(ii) – show that you get a Fresnel type of integral that when evaluated produces ψ(x, t). You are not expected to actually perform the evaluation.
(6 + 4) + (10 + 5) + 5 = 30 marks

Question 2. 量子物理作业代写
We are going to generalise the harmonic oscillator from one dimension to two dimensions x1 and x2. The Hamiltonian is given by
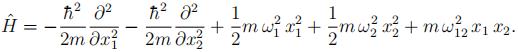
(i) For uncoupled oscillators, use separated-variables functions of the form f(x1)g(x2) to solve the energy eigenvalue problem. You may use the known result for the one-dimensional oscillator.
(ii) For the coupled case, the potential energy may be expressed in matrix notation as
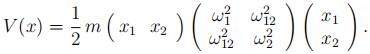
Taking inspiration from this, fifigure out a procedure for solving the general,coupled case. (You are not expected to actually do all of the algebra, just enough of it to explain the method.)
15 + 15 = 30 marks

更多代写:北美代考推荐 gmat online作弊 澳洲Cs网课代考 Summary摘要代写 论文润色 高级金融经济学代考
