副标题#e#
快速排序根基特性
时间巨大度:O(n*lgn)
最坏:O(n^2)
空间巨大度:最好环境下:O(lgn),最坏环境:O(n),平均环境:O(lgn)
不不变。
关于快速排序的空间巨大度,感谢@运气他爹 同学指正。详述一下。
快速排序由于每次递归的时候会占用一个空间返回中间数位置,所以一次递归的空间巨大度为O(1)。
最好环境和最坏环境下的递归深度为O(lgn),相应的空间巨大度就是O(lgn)
最坏环境下的递归深度为O(n),空间巨大度为O(n)。
算法
QUICKSORT(A, p, r)
if p < r
then q ← PARTITION(A, p, r) //要害
QUICKSORT(A, p, q - 1)
QUICKSORT(A, q + 1, r)
PARTITION(A, p, r)
x ← A[r]
i ← p - 1
for j ← p to r - 1
do if A[j] ≤ x
then i ← i + 1
exchange A[i] <-> A[j]
exchange A[i + 1] <-> A[r]
return i + 1
示例
待排序数组:7 3 5 9 8 5 1 10 4 6
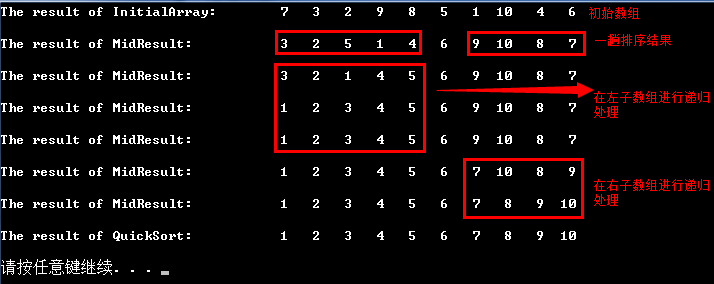
一趟排序进程阐明:
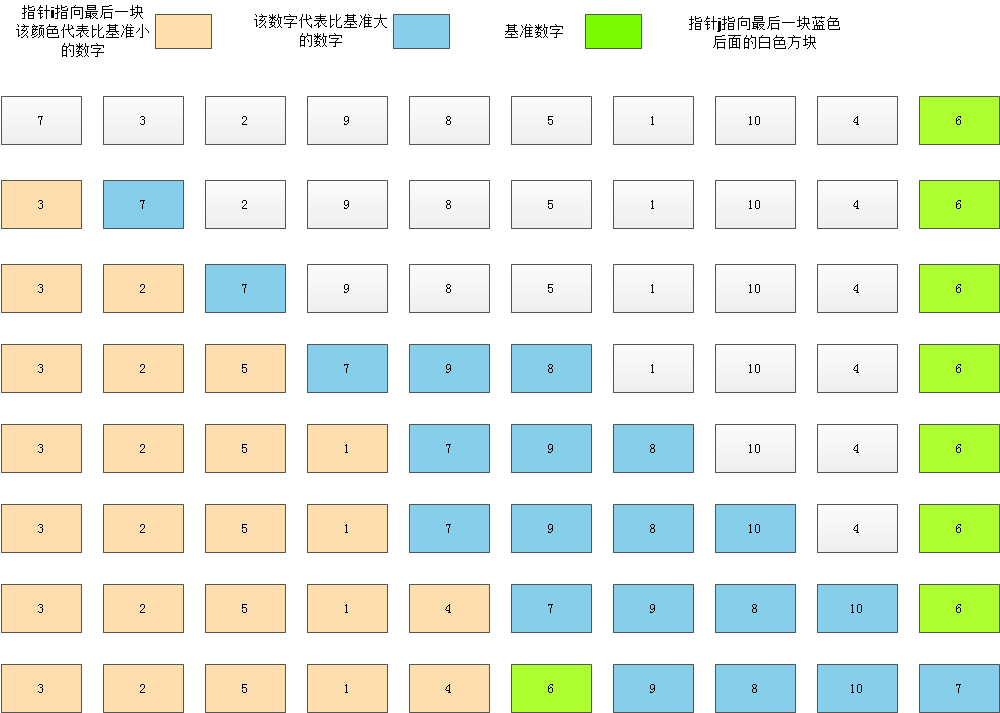
#p#副标题#e#
源码
类声明
class BaseSort {
public:
BaseSort() { }
virtual void sort() = 0;
};
class QuickSort : public BaseSort {
public:
QuickSort(int Array[], int len) : BaseSort() {
this->Array = Array;
this->len = len;
}
void sort();
private:
int partition(int Array[], int start, int end);
void quicksort(int Array[], int start, int end);
private:
int* Array;
int len;
};
相关成员函数实现
void QuickSort::sort() {
quicksort(Array, 0, len-1);
}
void QuickSort::quicksort(int Array[], int start, int end) {
if ( start < end ) {
int mid = this->partition(Array, start, end);
if ( start < mid - 1 )
quicksort(Array, start, mid-1 );
if ( mid + 1 < end )
quicksort(Array, mid+1, end);
}
}
int QuickSort::partition(int Array[], int start, int end) {
int i, j, x, tmp;
x = Array[end];
i = start -1;
for ( j = start; j < end; j++ ) {
if ( Array[j] <= x) {
i++;
tmp = Array[j];
Array[j] = Array[i];
Array[i] = tmp;
}
}
tmp = Array[end];
Array[end] = Array[i+1];
Array[i+1] = tmp;
if (DEBUG) {
printArray(Array, len, "MidResult");
}
return i+1;
}
测试:
int a[10] = {7,3,2,9,8,5,1,10,4,6};
int len = 10;
QuickSort* quicksort= new QuickSort(a, len);
quicksort->sort();
printArray(a, len, "QuickSort");
运行截图:

