Assign-Bootstrap-AE2
February 5, 2021
计量经济学网课代刷 Submit your work in the form of (i) a Jupyter Notebook and (ii) PDF-file via Canvas assum- ing basic econometric knowledge, before the deadline.
0.1 Programming Assignment – Bootstrap Methods – Adv. Econometrics 2 计量经济学网课代刷
Deadline: Friday 17:00 hours, 8 January 2021
Declaration of Originality
We whose names are given under 1., 2. and 3. above declare that:
1. These solutions are solely our own work.
2. We have not made (part of) these solutions available to any other student.
3. We shall not engage in any other activities that will dishonestly improve my results or dis- honestly improve or hurt the results of others.
0.2 Instructions for completing and submitting the assignment
1. Submit your work in the form of (i) a Jupyter Notebook and (ii) PDF-file via Canvas assum- ing basic econometric knowledge, before the deadline. Your notebook should not give errors when executed with Run All. 计量经济学网课代刷
2. Complete the table with the info of your group members. By submitting the Jupyter Note- book, you agree with the included declaration of originality. Do not copy work of others. This will be considered as fraud!
3. Clarify your code with comments.
0.3 Hints 计量经济学网课代刷
• Only use the paired bootstrap
• Work with Numpy vectors or matrices as much as possible,
e.g. np.quantile(tB_OLS,[0.05,0.95],axis=0) returns two quantiles for the whole vector of OLS estimates
• When coding, you can reduce the running time by setting BOOTREP=99 and reduce the num- ber of simulations. For the final execution, please return to original values!
• For a progress bar, please install conda install -c conda-forge tqdm or if you don’t use anaconda use can just execute pip install tqdm 计量经济学网课代刷
• If you want to use plotly, please install conda install -c plotly plotly
• Below, you can find Python code for generating the data and doing a simulation using multi- cores. To use multicores, you have to install multiprocess: conda install -c conda-forge multiprocess. Otherwise, execute pip install multiprocess
• The idea behind multiprocess is that each CPU core receives a sample, executes the resam- pling and returns the results. These results will be stored in one big list, which can be ana- lyzed after the simulation.

0.4 Assignment 计量经济学网课代刷
The purpose of this assignment is for you to gain practical experience with resampling methods. You will investigate several bootstrap confidence intervals for OLS and LASSO estimators. The DGP is given by:
• Xi ∼ N(0, Σ), Σ = (σij) ∈ Rp×p with σij = ρ|i−j|, βj = 0 for 1 ≤ j ≤ p − 15, βj = 0.5 for p − 14 ≤ j ≤ p − 10, βj = 1.5 for p − 9 ≤ j ≤ p − 5 βj = 2.5 for p − 4 ≤ j ≤ p.
• ε1, …, εn ∼ N(0, 1)
• y = Xβ + ε
Let βˆ = (Xj X)−1 Xj y denote the OLS estimator, while β˘ denote the LASSO estimator based on minimizing
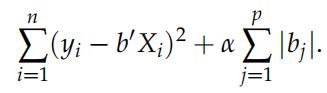
∑(yi − bj Xi)2 + α ∑ |bj|.
i=1 j=1
Only consider lasso = linear_model.Lasso(alpha=0.02), so keep the amount of regularization fixed!
Please, briefly answer all questions below using graphs and if necessary tables.
1. Choose n = 50, p = 25 and ρ = 0.6. Determine the bias and RMSE of the OLS and LASSO estimators using 1,000 Monte Carlo replications.
2. Estimate by simulation the coverage probabilities (cov. prob.) of the 90% first-order asymp- totic two-sided confidence intervals for the OLS estimator, i.e. the fraction of confidence intervals (CI) 计量经济学网课代刷
[βˆj − 1.645SE(βˆj ), βˆj + 1.645SE(βˆj )]that contains the true parameter βj. Here SE(βˆj ) is the usual (non-robust) standard error based on s2(Xj X)−1.
3. Estimate by simulation the cov. prob. of the 90% first-order asymptotic two-sided CI for OLS and LASSO using
SEboot(β˜),
for β˜ ∈ {βˆ, β˘}.$
4. Note that the cov. prob. can be interpreted as the number of successes in 1,000 trials. Hence, the estimated cov. prob. is not significantly different (at the 95% confidence level) from 90% if its value is contained in the interval
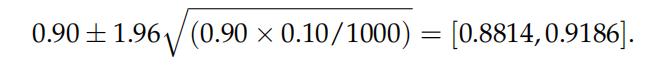
Check if the estimated cov. prob. of questions 2 & 3 are significantly different from 90%. What is your conclusion?
5. Estimate by simulation the cov. prob. for OLS and LASSO of 90% equal-tailed two-sided percentile bootstrap confidence intervals:
(β˜∗95%, β˜∗5%),
where P∗[β˜∗ > β∗5%] = 5% and β˜ ∈ {βˆ, β˘}.
6. Estimate by simulation the cov. prob. for OLS of 90% equal-tailed two-sided percentile-t bootstrap confidence intervals based on the quantiles of the root
(βˆ∗ − βˆ)/SE(βˆ∗ ), where SE(βˆ∗ ) is based on s∗2(X∗ j X∗ )−1.
7. What problems would you encounter if you wanted to implement the percentile-t intervalsfor the LASSO? How could you remedy these problems (you don’t have to implement this)? 计量经济学网课代刷
8. Estimate by simulation the cov. prob. for LASSO of 90% two-sided bias-corrected and ac- celerated (BCa) confidence intervals. For this, use the bootstrap to estimate the (median) bias and the Jackknife for the acceleration constant. In the BCa method, the quantiles are adjusted:
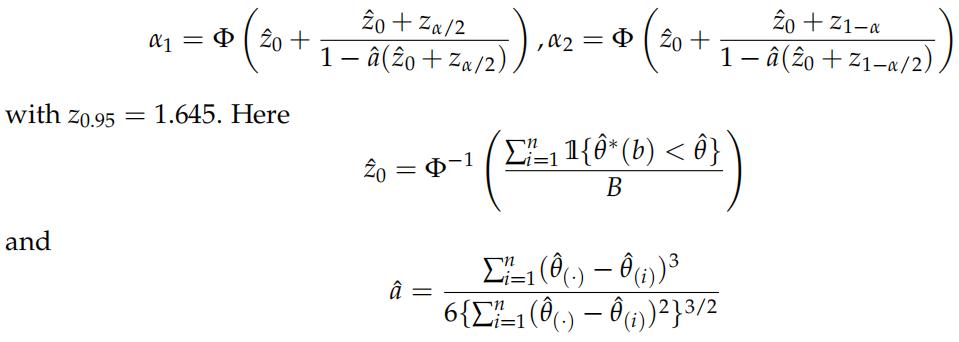
with θˆ( ) = ∑n 1 θˆ(i)/n; see for more details Section 14.3 of Efron, B., & Tibshirani, R. J. (1994). An introduction to the bootstrap: link).
9. Based on all the results of this assignment, which inference procedure would you advise a practitioner that wants to conduct inference in a model described by the DGP? Motivate your recommendation.
0.5 Generate Samples 计量经济学网课代刷
0.6 Resampling Procedure


0.7 Execute the Simulation and get Results 计量经济学网课代刷
[4]: [4]: from multiprocess import Poolpool4 = Pool(processes=4)
result_list = list(tqdm(pool4.imap_unordered(Bootstrap, arglist), total=REP)
6pool4.close()
pool4.join()
HBox(children=(FloatProgress(value=0.0, max=1000.0), HTML(value=”)))
0.8 Perform the Post-Processing
0.9 Carry Out Analysis 计量经济学网课代刷

0.10 Question 1 计量经济学网课代刷
1. Choose n = 50, p = 25 and ρ = 0.6. Determine the bias and RMSE of the OLS and LASSO estimators using 1,000 Monte Carlo replications.
The bias and RMSE of the OLS and LASSO estimators are shown below in a chart
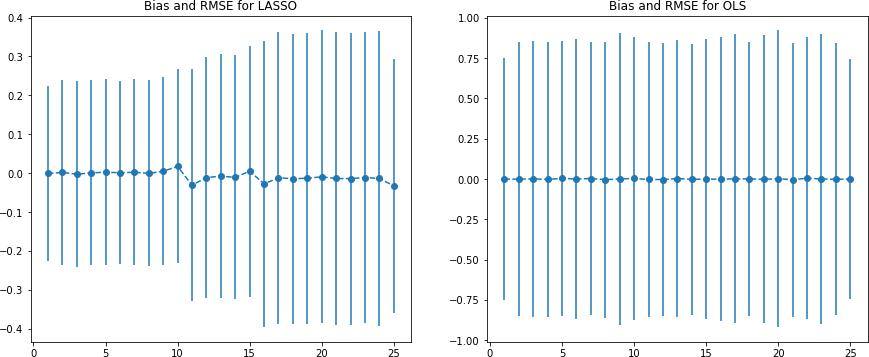
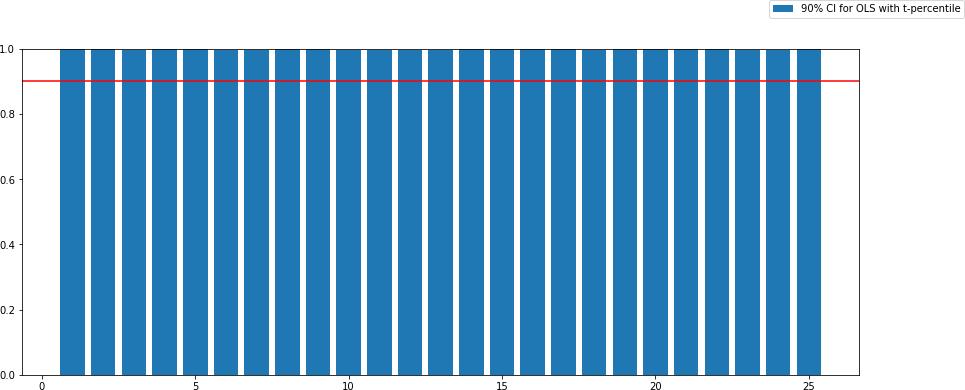
0.11 Question 2
2. Estimate by simulation the coverage probabilities (cov. prob.) of the 90% first-order asymp- totic two-sided confidence intervals for the OLS estimator, i.e. the fraction of confidence intervals (CI)
[βˆj − 1.645SE(βˆj ), βˆj + 1.645SE(βˆj )]that contains the true parameter βj. Here SE(βˆj ) is the usual (non-robust) standard error based on s2(Xj X)−1.

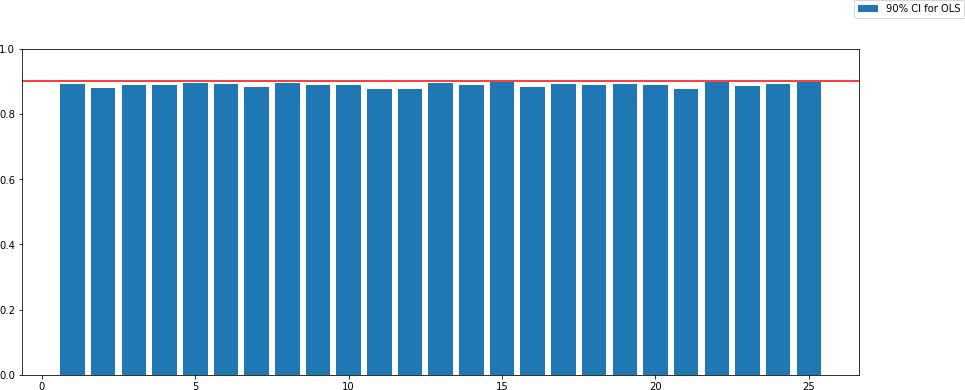
The cov. prob. using standard deviation is 计量经济学网课代刷
[0.891 0.879 0.887 0.887 0.895 0.893 0.883 0.894 0.889 0.887 0.876 0.8770.895 0.887 0.897 0.883 0.892 0.888 0.891 0.888 0.877 0.897 0.884 0.893
0.898]
0.12 Question 3 计量经济学网课代刷
3. Estimate by simulation the cov. prob. of the 90% first-order asymptotic two-sided CI for OLS and LASSO using
SEboot(β˜),
for β˜ ∈ {βˆ, β˘}.$

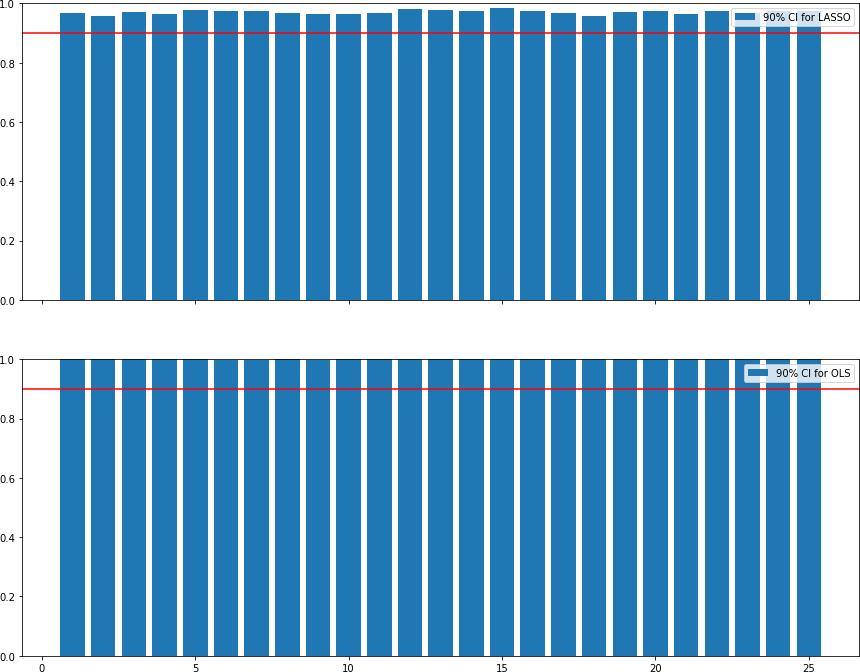


0.13 Question 4
4. Note that the cov. prob. can be interpreted as the number of successes in 1,000 trials. Hence, the estimated cov. prob. is not significantly different (at the 95% confidence level) from 90% if its value is contained in the interval
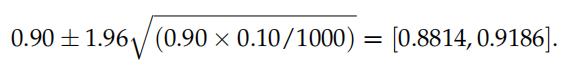
Check if the estimated cov. prob. of questions 2 & 3 are significantly different from 90%. What is your conclusion? 计量经济学网课代刷
The cov. prob. in question 2 were very close to 90%. But the cov. prob. estimated in part 3 were significantly different from 90%.
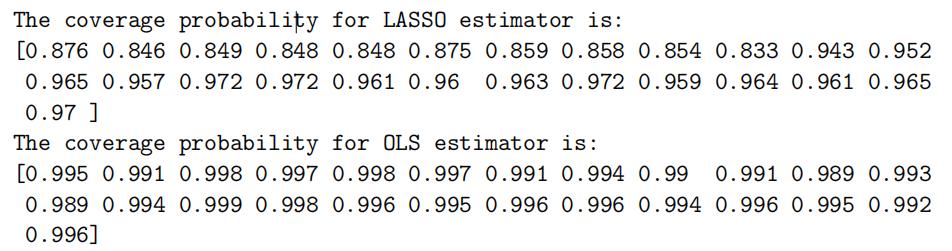
0.14 Question 5 计量经济学网课代刷
5. Estimate by simulation the cov. prob. for OLS and LASSO of 90% equal-tailed two-sided percentile bootstrap confidence intervals:
(β˜∗95%, β˜∗5%),
where P∗[β˜∗ > β∗5%] = 5% and β˜ ∈ {βˆ, β˘}.

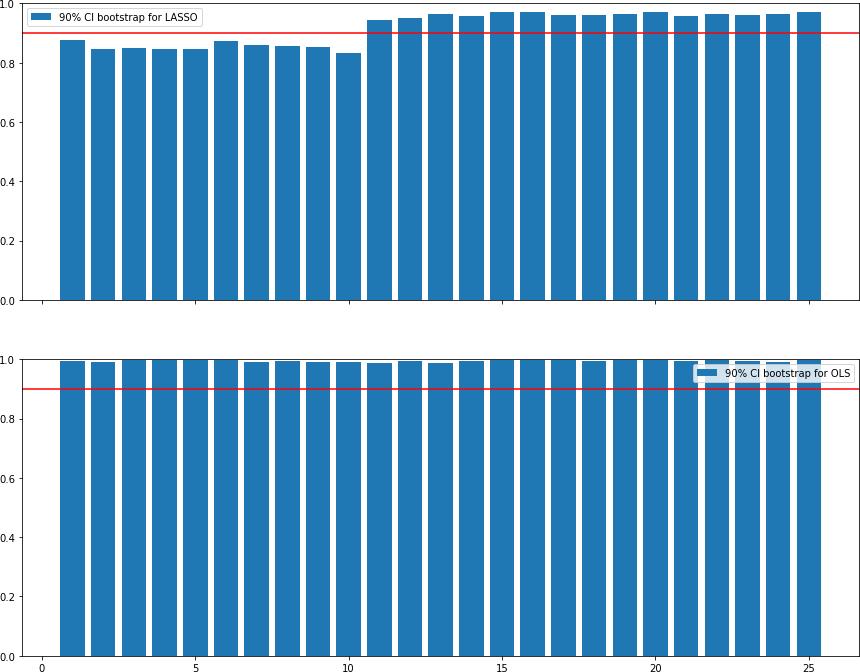
0.15 Question 6
6. Estimate by simulation the cov. prob. for OLS of 90% equal-tailed two-sided percentile-t bootstrap confidence intervals based on the quantiles of the root
(βˆ∗ − βˆ)/SE(βˆ∗ ),
where SE(βˆ∗ ) is based on s∗2(X∗ j X∗ )−1. 计量经济学网课代刷



0.16 Question 7
7. What problems would you encounter if you wanted to implement the percentile-t intervalsfor the LASSO? How could you remedy these problems (you don’t have to implement this)?
The problem would be that some coefficients will be estimated to be zero all the time, then their SE will be zero as well. In this case, the t statistic is not defined. We may change the formula to add a very small non-zero value to the nominator.
0.17 Question 8
8. Estimate by simulation the cov. prob. for LASSO of 90% two-sided bias-corrected and ac- celerated (BCa) confidence intervals. For this, use the bootstrap to estimate the (median) bias and the Jackknife for the acceleration constant. In the BCa method, the quantiles are
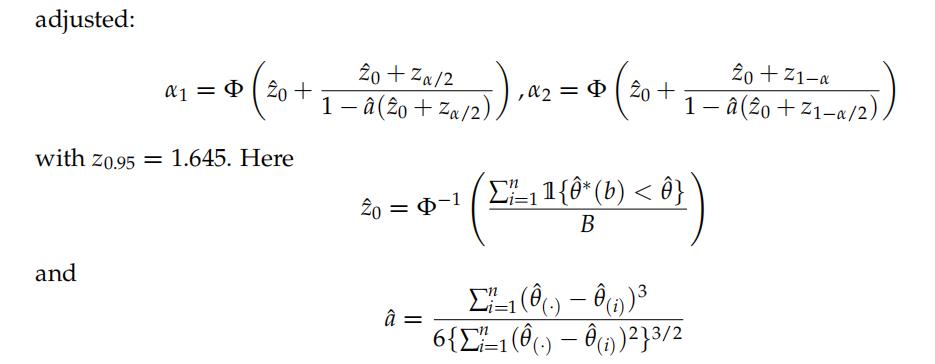
with θˆ( ) = ∑n 1 θˆ(i)/n; see for more details Section 14.3 of Efron, B., & Tibshirani, R. J. (1994). An introduction to the bootstrap: link). 计量经济学网课代刷

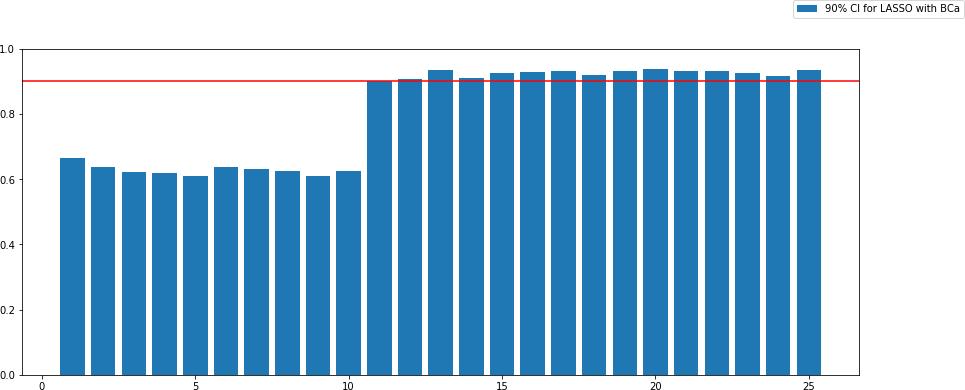
The cov. prob. using BCa is
[0.666 0.637 0.622 0.619 0.611 0.638 0.631 0.624 0.608 0.625 0.902 0.9080.935 0.91 0.926 0.929 0.932 0.919 0.93 0.937 0.93 0.932 0.926 0.916
0.936]
0.18 Question 9
9. Based on all the results of this assignment, which inference procedure would you advise a practitioner that wants to conduct inference in a model described by the DGP? Motivate your recommendation.
I will recommend the asymptotic two-sided confidence interval, with the standard deviation de- rived from bootstrap. From the experiment, we can see that this method works the best by pro- viding the best confidence interval.
[ ]:
更多代写:Stata程序代做 quiz代考价格 Nursing Essay代写润色 Nursing Essay代写 Music音乐论文代写 经济论文代写
