副标题#e#
看过这样一道题,问,“措施布局化设计的三种基本布局,顺序、选择、轮回是不是必需的?”虽然,你知道这样一个论断,只要有这三种就足够了;可是能不能更少呢?谜底是“可以”,原因就是递归能代替轮回的浸染,譬喻下面的对一个数组内里元素求和的函数:
float rsum (float a[], const int n)
{
if (n <= 0) return 0;
else return rsum(a, n – 1) + a[n – 1];
}
实际上就是:
sum = 0;
for (int i = 0; i < n; i++) sum += a[i];
但实际的环境是,任何的一种语言内里都有轮回布局,但不是任何的语言都支持递归;套用一句话,递归是万能的,但没有递归不是万万不能的。然而,我看到此刻的某些人,不管什么问题都要递归,显着轮回是第一个想到的要领,偏偏费尽头脑去寻找递归算法。对此,我真的不知道该说什么。
递归是算法吗
常常的看到“递归算法”、“非递归算法”,这种提法没有语义上的问题,而且我本身也这样用——递归的算法。但这也正说明白,递归不是算法,他是一种思想,正是因为某个算法的指导思想是递归的,所以才被称为递归算法;而一个有递归算法的问题,当你不利用递归作为指导思想,这样获得的算法就长短递归算法。——而对付轮回能处理惩罚的问题,都有递归解法,在这个意义上说,轮回算法都可以称为非递归算法。
我在这咬文嚼字没什么此外意思,只是想让各人知道,能写出什么样的算法,要害是看你编写算法时的指导思想。假如一开始就想到了轮回、迭代的要领,你再操心耗神去找什么递归算法——纵然找到了一种看似“简捷”的算法,由于他的低效实际上照旧废料——你还在做这种无用功干什么?典范的学究成规。假如你仅仅想到了递归的要领,此刻你想用栈来消解掉递归,你做的事情仅仅是把系统做的事本身做了,你又能把效率提高几多?盲目标迷信消解递归就必然能提高效率是无按照的——你做的事情的要领假如不恰当的话,甚至还不如系统本来的做法。
#p#副标题#e#
从学分列组合那天开始,我所知道的阶乘就是这个样子n! = 1×2×……n。假如让我来写阶乘的算法,我也只会想到从1乘到n。再如,斐波那契数列,假如有人用自然语言描写的话,必然是这样的,开始两项是0、1,今后的每项都是前面两项的和。所以让我写也只会获得“生存前两项,然后相加获得功效”的迭代解法。——此刻只要是讲到递归险些就有他们的登场,美其名曰:“界说是递归的,所以我们写递归算法”。我想问的是,界说的递归抽象是从那边来的?显然阶乘的界说是从一个轮回进程抽象来的,斐波那契数列的界说是个迭代的抽象。于是,我们先从一个本不是递归的事实抽象出一个递归的界说,然后我们说,“因为问题的界说是递归的,因此我们很容易写出递归算法”,接着说,“我们也能将这个递归算法转化为轮回、迭代算法”,给人的感受就像是1÷3=0.33……,0.33……×3=0.99……,然后我们花了好大的心智才大白1=0.99……。
照旧有那么些人乐此不疲,是凡讲到递归就要提到这两个,功效,没有一个学生看到阶乘那样界说没有疑问的,没有一个对付谁人递归的阶乘函数抱有钦佩之情的——瞎折腾什么呢?所以,假如要讲递归,就要一个令人信服的例子,而这个例子非汉诺塔莫属。
汉诺塔的非递归解法
好像这个问题的最佳解法就是递归,假如你想用栈来消解掉递归到达形式上的消除递归,你照旧在利用递归的思想,因此,他本质上照旧一个递归的算法。我们这本黄皮书在谈论到“什么环境利用递归”的时候,在“3.问题的解法是递归的”这内里,就这样说了“有些问题只能用递归的要领来办理,一个典范的例子就是汉诺塔”。
但我坚信,假如一个问题能用阐明的步伐办理——递归实际上就是一个阐明解法,能将问题解析成-1局限的同等问题和移动一个盘子,假如这样解析下去必然会有解,最后解析到移动1号盘子,问题就办理了——那么我也应该能用综合的步伐办理,就是从当前的状态来确定奈何移动,而不是逆推获得抉择。这是对实际事情进程的一个模仿,试想假如让我们去搬盘子,我们必定不会用递回来思考此刻应该怎么搬——只要8个盘子,我们脑筋里的“事情栈”恐怕就要溢出了——我们要当即抉择怎么搬,而不是从几多步之后的情景来知道怎么搬。下面我们通过模仿人的正向思维来寻找这个解法。

#p#分页标题#e#
假设如下搬7个盘子的初始状态(选用7个是因为我曾经写出了一个1~6功效正确的算法,而在7个的时候才发明一个条件的选择错误,详细各人本身实验吧),我们独一的选择就是搬动1号盘子,可是我们的问题是向B搬照旧向C搬?
显然,我们必需将7号盘子搬到C,在这之前要把6号搬到B,5号就要搬到C,……以此类推,就会得出结论(纪律1):当前柱最上面的盘子的方针柱应该是,从当前柱上“需要搬动的盘子”最下面一个的方针柱,向上瓜代互换方针柱到它时的方针柱。就是说,假如当前柱是A,需要移动m个盘子,从上面向下数的第m个盘子的方针柱是C,那么最上面的盘子的方针柱就是这样:if (m % 2) 方针和第m个盘子的方针沟通(C);else 方针和第m个盘子的方针差异(B)。接下来,我们需要思量假如产生了阻塞,该怎么办,如下所示:
3号盘子的方针柱是C,可是已经有了1号盘子,我们最直觉的反应就是——将碍事的盘子搬到另一根柱子上面去。于是,我们要做的是(纪律2):生存当前柱的信息(柱子号、应该搬动的最下面一块盘子的号,和它的方针柱),以备当障碍排除后回到此刻的柱子继承搬,将当前柱转换为碍事的盘子地址的柱子。假设这样若干步后,我们将7号盘子从A搬到了C,此时,生存当前柱号的栈必然是空了,我们该怎么办呢?
显而易见的,转换当前柱为B,把6号盘子搬到C。由此可得出(纪律3):假设当前的问题局限为n,搬动第n个盘子到C后,问题局限减1,当前柱转换到另一个柱子,最下面的盘子的方针柱为C。
综上,我们已经把这个问题办理了,可以看出,要害是如何确定当前柱需要移动几多盘子,这个问题请各人本身思量,给出如下例程,因为没有颠末任何优化,本人的编码程度又较量低,所以这个函数很慢——比递归的还慢10倍。
#include <iostream>
#include <vector>
using namespace std;
class Needle
{
public:
Needle() { a.push_back(100); }//每一个柱子都有一个底座
void push(int n) { a.push_back(n); }
int top() { return a.back(); }
int pop() { int n = a.back(); a.pop_back(); return n; }
int movenum(int n) { int i = 1;while (a[i] > n) i++; return a.size() - i; }
int size() { return a.size(); }
int operator [] (int n) { return a[n]; }
private:
vector<int> a;
};
void Hanoi(int n)
{
Needle needle[3], ns;//3个柱子,ns是转换柱子时的生存栈,借用了Needle的栈布局
int source = 0, target, target_m = 2, disk, m = n;
for (int i = n; i > 0; i--) needle[0].push(i);//在A柱上放n个盘子
while (n)//问题局限为n,开始搬动
{
if (!m) { source = ns.pop(); target_m = ns.pop();
m = needle[source].movenum(ns.pop()); }//障碍盘子搬走后,回到本来的当前柱
if (m % 2) target = target_m; else target = 3 - source - target_m;//纪律1的实现
if (needle[source].top() < needle[target].top())//当前柱顶端盘子可以搬动时,移动盘子
{
disk = needle[source].top();m--;
cout << disk << " move " << (char)(source + 0x41) << " to "<< (char)(target + 0x41) << endl;//显示搬动进程
needle[target].push(needle[source].pop());//在方针柱上面放盘子
if (disk == n) { source = 1 - source; target_m = 2; m = --n; }纪律3的实现
}
else//纪律2的实现
{
ns.push(needle[source][needle[source].size() - m]);
ns.push(target_m); ns.push(source);
m = needle[target].movenum(needle[source].top());
target_m = 3 - source - target; source = target;
}
}
}
这个算法实现比递归算法巨大了许多(递归算法在网上、书上随便都可以找到),并且还慢许多,好像是多余的,然而,这是有现实意义的。我不知道此刻还在搬64个盘子的和尚是怎么搬的,不外我意料必然不是先递归到1个盘子,然后再搬——等递归出来,预计胡子一打把了(能不能在人世还两说)。我们必然是顿时抉择下一步怎么搬,就如我上面写的那样,这才是人的正常思维,而用递回来思考,想出来怎么搬的时候,黄瓜菜都凉了。正像我们干事的要领,固然我此生当代完不成这项事业,但我必然要为后人完成我能完成的,而不是在那梦想后人应该怎么完成——假如达不到最终的功效,那也必然担保向正确的偏向前进,而不是呆在原地梦想。
#p#分页标题#e#
由此看出,计较机编程实际上和正常的干事步调的差距照旧很大的——我们的干事步调假如直接用计较机来实现的话,其实并不能最优,原因就是,实际中的相关性在计较机中大概并不存在——好比人脑的逆推深度是有限的,而计较秘密比人脑深许多,论影象的精确性,计较秘密比人脑强许多。这也导致了一个普通的措施员和一个资深的措施员写的算法的速度经常有天壤之别。因为,后者知道计较机喜欢怎么思考。
迷宫
关于迷宫,有一个引人入胜的希腊神话,这也是为什么现今每当人们提到这个问题,老是兴致勃勃(对付年轻人,预计是RPG玩多了),正如固然九宫图连小学生都能做出来,我们老是孤高的说那叫“洛书”。这个神话我不复述了,有乐趣的可以在搜索引擎上输入“希腊神话 迷宫”,就能找到许多的先容。
迷宫的神话报告了一位英雄如何靠着“线团”杀死了牛头怪(玩过《英雄无敌》的伴侣必然知道要想造牛头怪,就必需建迷宫,也是从这里来的),我看到的一本编程书上援引这段神话报告迷宫算法的时候,不知是有意杜撰,照旧考据不严,把这个进程论述成:英雄靠着线团的辅佐——在走过的路上铺线,每到分岔口向没铺线的偏向前进,假如碰着死胡同,沿铺的线返回,并铺第二条线——走进了迷宫深处,杀死了牛头怪。然而,神话传说讲的是,英雄被当成贡品和其他的孩子送到了迷宫的深处,英雄杀死了牛头怪,靠着线团标识的蹊径退出了迷宫。实际上,这个线团只是个“栈”,远没有现代人赋予给它的“神奇浸染”。我想作者也是RPG玩多了,总想着奈何“勇者斗恶龙”,然而,实际上却是“胜利大逃亡”。
迷宫问题实际上是一个心理测试,它反应了测试者节制心理不变的本领——在一次次失败后,是否失去沉着最终陷在迷宫之中,也正浮现了一句诗,“不识庐山真脸孔,只缘身在此山中”。换而言之,我们研究迷宫的计较机解法,并没有什么意义,迷宫就是为人设计的,而不是为呆板设计的,它之所以称为“迷”宫,前提是人的影象精确性不足高;假设人有呆板那样的精确的影象,只要他不傻,都能走出迷宫。此刻大概有人用智能呆板人的研究来辩驳我,实际上,智能呆板人是在更高的层面上模仿人的思考进程,只要它完全再现了人的寻路进程,它就能走出迷宫。可是,研究迷宫生成的计较秘密领,却是有意义的,因为人们老是有凌虐本身的倾向(不少人在RPG里的迷宫转了三天三夜也不知道倦怠)。
不管怎么说,照旧亲自研究一下计较机怎么走迷宫吧。
迷宫的存储
凭据老例,用一个二维数组来暗示迷宫,0暗示墙,1暗示通路,今后我们的措施都走下面这个迷宫。
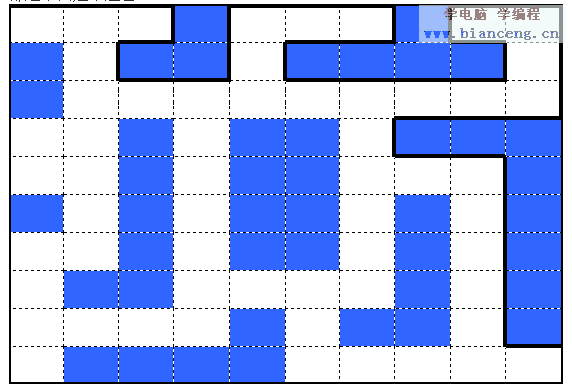
递归法和回溯法
有人说,回溯实际上是递归的展开,但实际上。两者的指导思想并纷歧致。
打个例如吧,递归法比如是一个部队要通过一个迷宫,到了第一个分岔口,有3条路,将军呼吁3个小队别拜别探哪条路能到出口,3个小队沿着3条路别离前进,各自达到了路上的下一个分岔口,于是小队长再分配人手各自去探路——只要人手足够(比较而言,就是计较机的仓库足够),最后必将有人找到出口,从这人开始只要层层上报直属率领,最后,将军将获得一条通路。所差异的是,计较机的递归法是把这个并行进程串行化了。
而回溯法例是一小我私家走迷宫的思维模仿——他只能寄但愿于本身的影象力,假如他没有步伐在分岔口留下标志(电视里一演到什么迷宫寻宝,总有恶人去改大好人的标志)。
想到这里溘然有点大白为什么都喜欢递归了,他可以或许满意人心最底层的虚荣——莫非你不以为利用递归就象谁人分配士兵的将军吗?想想汉诺塔的解法,也有这个倾向,“你们把上面的N-1个拿走,我就能把下面的挪已往,然后你们在把那N-1个搬过来”。笑谈,切勿卖力。
#p#分页标题#e#
这两种要领的例程,我不给出了,网上许多。我只想对书上的递归解法颁发点观点,因为书上的解法有偷梁换柱的嫌疑——迷宫的储存不是用的二维数组,居然直接用岔路口之间的毗连暗示的——的确是工钱的低落了问题的难度。实际上,假如把迷宫抽象成(岔路口)点的毗连,迷宫就酿成了一个“图”,求解进口到出口的蹊径,完全可以用图的遍历算法来办理,只要从进口DFS到出口就可以了;然而,从二维数组暗示的迷宫转化为图是个很巨大的进程。而且这种转化,实际上就是没走迷宫之前就知道了迷宫的布局,显然是不公道的。对此,我只能说这是为了递归而递归,然后还本身给本身开绿灯。
但迷宫并不是只能用上面的要领来走,前提是,迷宫只要走出去就可以了,不需要找出一条大概上的最短蹊径——确实,迷宫只是前进中的障碍,一旦走通了,没人走第二遍。下面的要领是一位游戏玩家提出来的,既不需要递归,也不需要栈往返溯——玩游戏照旧有收获的。
另一种解法
请留意我在迷宫顶用粗线描出的蹊径,实际上,在迷宫中,只要从进口始终沿着一边的墙走,就必然能走到出口,那位玩家称之为“靠一边走”——假如你不把迷宫的通路当作一条线,而是一个有面积的图形,很快你就知道为什么。编程实现起来也很简朴。
下面的措施在TC2中编译,不能在VC6中编译——为了动态的表示人的移动环境,利用了gotoxy(),VC6是没有这个函数的,并且堆砌迷宫的219号字符是不能在利用中文页码的操纵系统的32位的console措施显示出来的。假如要在VC6中实现gotoxy()的成果还得用API,为了一个简朴的措施没有须要,所以,就用TC2写了,溘然换到C语言尚有点不适应。
#include <stdio.h>
typedef struct hero {int x,y,face;} HERO;
void set_hero(HERO* h,int x,int y,int face){h->x=x;h->y=y;h->face=face;}
void go(HERO* h){if(h->face%2) h->x+=2-h->face;else h->y+=h->face-1;}
void goleft(HERO* h){if(h->face%2) h->y+=h->face-2;else h->x+=h->face-1;}
void turnleft(HERO* h){h->face=(h->face+3)%4;}
void turnright(HERO* h){h->face=(h->face+1)%4;}
void print_hero(HERO* h, int b)
{
gotoxy(h->x + 1, h->y + 1);
if (b)
{
switch (h->face)
{
case 0: printf("%c", 24); break;
case 1: printf("%c", 16); break;
case 2: printf("%c", 25); break;
case 3: printf("%c", 27); break;
default: break;
}
}
else printf(" ");
}
int maze[10][10] =
{
0, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 0, 1, 1, 0, 1, 1, 1, 1, 0,
1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 1, 1, 0, 1, 1, 1,
0, 0, 1, 0, 1, 1, 0, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 1, 0, 1,
0, 0, 1, 0, 1, 1, 0, 1, 0, 1,
0, 1, 1, 0, 0, 0, 0, 1, 0, 1,
0, 0, 0, 0, 1, 0, 1, 1, 0, 1,
0, 1, 1, 1, 1, 0, 0, 0, 0, 0
};
void print_maze()
{
int i, j;
for (i = 0; i < 10; i++)
{
for (j = 0; j < 10; j++)
{
if (maze[i][j]) printf("%c", 219);
else printf(" ");
}
printf("\n");
}
}
int gomaze(HERO* h)
{
HERO t = *h; int i;
for (i = 0; i < 2; t = *h)
{
print_hero(h, 1); sleep(1); go(&t);
if (t.x >= 0 && t.x < 10 && t.y >= 0 && t.y < 10 && !maze[t.y][t.x])
{
print_hero(h, 0); go(h);/*前方可走则向前走*/
if (h->x == 9 && h->y == 9) return 1; goleft(&t);
if (h->x == 0 && h->y == 0) i++;
if (t.x >= 0 && t.x < 10 && t.y >= 0 && t.y < 10 && !maze[t.y][t.x]) turnleft(h);/*左方无墙向左转*/
}
else turnright(h);/*前方不行走向右转*/
}
return 0;
}
main()
{
HERO Tom;/*有个英雄叫Tom*/
set_hero(&Tom, 0, 0, 0);/*放在(0,0)面朝北*/
clrscr();
print_maze();
gomaze(&Tom);/*Tom走迷宫*/
}
总结
书上讲的根基上就这些了,要是细说起来,几天几夜也说不完。前面我并没有讲如何写递归算法,实际上给出的都长短递归的要领,我也以为有点文差池题。我的目标是使各人大白,能写出什么算法,主要看你办理问题的指导思想,换而言之,就是对问题的认识水平。所以初学者此刻就去追求“大度”的递归算法,是不现实的,功效往往就是削足适履,搞的一团糟——有位仁兄写了个骑马游世界的“递归”措施,在我呆板上10分钟没反应。其实优秀的递归算法是在对问题有了清楚的认识后才会得出的。
