MT3502 Real Analysis – Problem Set
实分析代写 1 Sets, functions, numbers – revision 1.2Establishwhich of the following functions are injections, surjections and Find the inverses o
1 Sets, functions, numbers – revision
1.1
Forall n = 1, 2, 3, . . . let Xn ⊆ R be the open interval (1/n, 2 + 1/n). Find
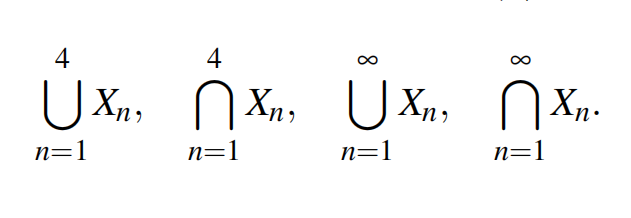
1.2
Establishwhich of the following functions are injections, surjections and Find the inverses of any bijections (except for parts (g) and (h)).
(a) f : R→ R f (x) = x2 (b) f : R → R f (x) = x3
- (c) f : Z → Z f (x) = x2 (d) f : Z → Z f (x) = x3(e) f : Z → Z f (x) = x + 7 (f) f : N → N f (x) = x + 7(g) f : R → R f (x) = x3 + 9x (h) f : R → R f (x) = x3 − 9x.
1.3
Let f : X → Y be a function and A, B ⊆ X Showthat
f (A ∪ B) = f (A) ∪ f (B),
f (A ∩ B) ⊆ f (A) ∩ f (B).
Give and example to show that “⊆” cannot be replaced by”=” in the second case.
1.4 实分析代写
Letf : A → B and g : B → C be Show that the composition g ◦ f : A → C is a bijection. Express (g ◦ f )−1 : C → A in terms of f −1 and g−1.
1.5
For each of the following relations R, determine whether R is reflexive, symmetric, and transitive. For those that are equivalence relations, describe the equivalence
(a) On R, xRy if x ≤y.
(b) On N, xRy if x is a multiple of y.
(c) OnR × R, (x, y)R(r, s) if x2 + y2 = r2 + s2.
(d) On C, zRw if Re(z) =Re(w).
2 Countable and uncountable sets 实分析代写
2.1
Let A = { a +bi : a, b∈N} , i.e. the set of complex numbers with real and imaginary parts both positive Show that A is countable by each of the following methods:
(i) by enumerating the elements of A as alist,
(ii) by defining an injection from A toN,
(iii) by finding a known countable set (i.e. one discussed in the notes) similar to A.
2.2
Determine, giving brief reasons (you may quote any standard results from the notes), whether each of the following sets is countable or uncountable
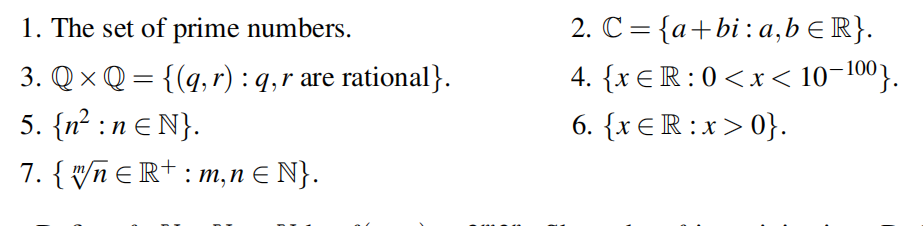
2.3
Define f : N × N → N by f (m, n) =2m3n. Show that f is an injection. Deducethat N × N is countable.
Now define f : {finite subsets of N}→ N by f ({i1, i2, . . . , ik}) = pi1 pi2 ··· pik where pi is the ith prime number. Show that f is an injection. Deduce that the set of all finite subsets of N is countable.
2.4 LetA = {(a1, a2, . . .) : ai Z for all i }, i.e. the set of all sequences of integers. Use Cantor’s diagonal argument to show that A is uncountable.

2.6
LetC be the middle-third Cantor set, that is the set of all numbers in [0, 1] whose base 3 expansion uses only the digits 0 and 2. Show that C is uncountable. Sketch the set C. (Hint: Consider the numbers whose first digit is 0 or 2, then the numbers whose second digit is 0 or 2, and so on.) What is the ‘length’ of C? (use the obvious definition of length so that an interval [a, b] or (a, b) has length b − a).
3 Convergence, continuity, uniform continuity 实分析代写
Infs and Sups

3.3 Let X ,Y be non-empty sets of real numbers. Show from the definition of supremum thatsup(X + Y ) = sup X + supY , where X + Y = {x + y : x ∈ X , y ∈ Y }.
Find a counter-example to show that sup(XY ) = sup X supY is generally false, where XY = {xy : x ∈ X , y ∈ Y }.
Convergence of sequences

Continuous functions
3.8 Showfrom the definition of continuity that the following functions are continuous.
(a) f : [0, 1] → R given by f (x) = 1/(1 + x2),
(b) f: R → R given by f (x) = |x| [Hint: reverse triangle inequality],
(c) f: R → R given by f (x) = x3.
3.9 Show (a) from the definition of continuity and (b) using sequences that,if f , g : [a, b] → R are continuous at c ∈ [a, b], then 2 f + 3g is continuous at c.
3.10 Let M > 0 and let f : R → Rsatisfy
| f (x) − f (y)| ≤ M|x − y| for all x, y ∈ R.
Show that f is continuous.
Deduce that ‘cos’ is a continuous function.
3.11 Let f : [0, 1] R be continuous with f (x) ∈ Q for all x ∈R. Show that f is a constant function, i.e. that there exists q ∈Q such that f (x) = q for all x ∈[0, 1]. [Hint: intermediate value theorem]

Uniform continuity
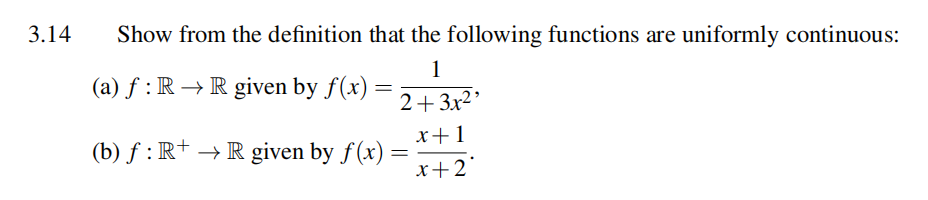
3.15 Show from the definition that the following functions are not uniformly continuous:
(a) f: R → R given by f (x) = x3,
(b) f: (0, 1) → R given by f (x) = 1/x.
3.16 Let M > 0 and let f: R → R be differentiable and such that f ‘(x) M for all x ∈ R. Show that f is uniformly continuous on R. [Hint: mean value theorem]
Deduce that f (x) = x2/(1 + x2) is uniformly continuous on R.
4 Integration 实分析代写
You may find it helpful to sketch graphs for many of the questions in this section.



5 Sequences and series of functions, power series 实分析代写
5.1
Definefn, f : [0, ∞) → R by fn(x) = x/(x + n) and f (x) = Show that:
(a) fn→ f pointwise,
(b) fn→ f uniformly on [0, 2],
(c) for all a > 0, fn→ f uniformly on [0, a],
(d) fndoes not converge uniformly to f on [0, ∞).
-
5.2
- Define fn, f : [0, ∞) → R by fn(x) = nx/(1 + nx) and f (x) = 1 (x > 0), f (0) = 0. Show that:
(a) fn→ f pointwise,
(b) fn→ f uniformly on [1, ∞),
(c) for all a > 0, fn→ f uniformly on [a, ∞),
(d) fn does not converge uniformly to f on [0, ∞). [Hint: use a standard result on uniform convergence.]
5.3
Define fn : [0,1] → R by fn(x) = xn(1−x). Show that fn → 0 uniformly. [Hint: you may need a different argument for x ‘close’ to 1 from other values of x.]



6 Metric and normed spaces 实分析代写
6.1 Which of the following define a metric on R? Justify your
(a) d(x, y) = x2 −y2,
(b) d(x, y) = |x2 −y2|,
(c) d(x, y) = |x3 −y3|.
6.2 Which of the following define a metric on R2? Justify your
(a) d ((x1, x2), (y1, y2)) = 3|x1 − y1| + 2|x2 − y2|,
(b) d ((x1, x2), (y1, y2)) = |x1 − y1||x2 − y2|,
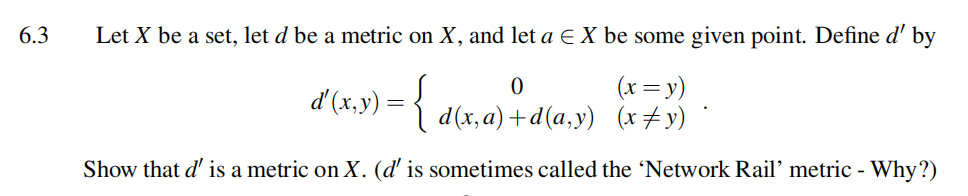
6.4
Let(X , d) be a metric Show that for all x, y, z, w ∈ X ,
(a) d(x, y) ≤ d(x, z) + d(z, w) + d(w, y),
(b) d(x, z) − d(y, z) ≤ d(x, y).

6.8 Let(X , d) be a metric Show from the definitions of metric and convergence that a sequence can have only one limit, i.e. if xn → x and xn → y then x = y.
6.9 Let(X , d) be a metric Show that if xn → x and yn → y then d(xn, yn) → d(x, y).
6.10 Showthat if xn → x in a normed space (X , ‖·‖ ) and scalars λn → λ, then λnxn → λx.

6.12 Let ‖‖1 and ‖‖2 both be norms on a vector space X . Show that ‖x‖ = ‖x‖1 + ‖x‖2 also defines a norm on X . Show that a sequence (xn) converges to (x) in ‖‖ if and only if it converges to x in both‖‖1 and ‖‖2.
6.13
Showfrom the definition that the following are Cauchy sequences:
(a) (n/(2n + 1)) in (R, | |),
(b) fn(t) = tn in (C[0, 1], ‖‖1).
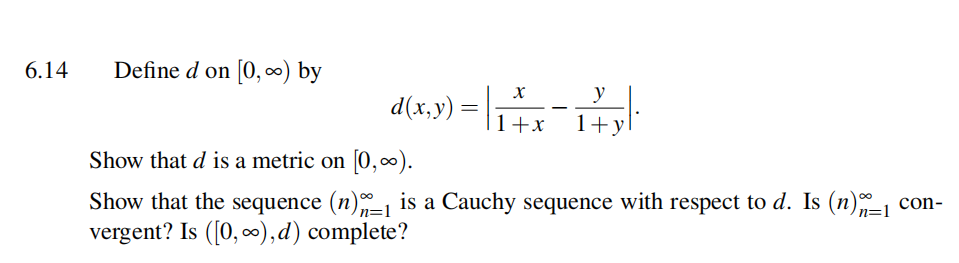
6.15 Let ‖‖1and ‖‖2 be equivalent norms on a vector space X , i.e there are constants a, b > 0 such that a‖x‖1 ≤ ‖x‖2 ≤ b‖x‖1 for all x ∈ X . Show that a sequence (xn) converges to x in ‖‖1 if and only if it converges to x in ‖‖2. Similarly, show that a sequence (xn) is Cauchy in ‖‖1 if and only if it is Cauchy in ‖‖2. Deduce that X is complete with norm ‖‖1 if and only if it is complete with norm ‖‖2.
6.16 Using the previous question, and the fact that (RN , ‖‖1) is complete (shown in lec- tures)show that (RN , ‖‖2) and (RN , ‖‖∞) are complete.


更多代写:计算机代上网课推荐 GMAT代考 英国Assignment统计学代写 留学生作业essay代写 留学生高中论文代写 代写accounting

