Midterm
决策模型和分析代考 #P = expected price next year for the stock #C = current number of shares for the stock #CPi = current price of the stock #C = purchase cost
Question 1 决策模型和分析代考
DECISION VARIABLES:
Xi, for number of shares to sell i=1,2,3 tech, bio, airline
OBJECTIVE FUNCTION:
Maximize ∑ Pi * (Ci-Xi)
#P = expected price next year for the stock #C = current number of shares for the stock
CONSTRAINTS:
#CPi = current price of the stock #C = purchase cost
∑ (Xi * CPi – Xi(CPi – Ci)*0.3 – Xi*CPi *0.01) ≥ 150,000
Xi ≥ 0, for all i=1, 2, 3
Question2 决策模型和分析代考
(a)
DECISION VARIABLES: Xij, i=1-9, j=1-8
Xij = 1, if driver i picks up rider j Xij = 0, otherwise
OBJECTIVE FUNCTIONS: to minimize total ETA
#ETA : estimated time of arrival
#Extra: extra time from picking up sharing riders
Extrai = 1, if more than 1 customer 决策模型和分析代考
Extrai = 0, otherwise
Min [∑∑(ETAij Xij) + Extra1 + Extra2]
CONSTRAINTS:
Xij binary 1<=i<=9, 1 <= j <=8
∑8𝑗=0𝑋𝑖𝑗 <=2 for each i=1,2
∑8𝑗=0𝑋𝑖𝑗 <=1 for each i=3,4,….9
∑𝑋𝑖𝑗9𝑖=0 =1 for each j=1,2,3…8
<=2 for each i=1,2
<=1 for each i=3,4,….9
=1 for each j=1,2,3…8
(b)
Minimum sum of ETA : 53 决策模型和分析代考
Matching:
Driver 1: rider 1, 8
Driver 3: rider 2
Driver 5: rider 3
Driver 6: rider 4
Driver 7: rider 5
Driver 8: rider 6
Driver 9: rider 7

Question3
DECISION VARIABLES:
Xij, i=1-12, j=1,2,3 (small, medium, large)
OBJECTIVE FUNCTIONS: to maximize total revenue
Maximize (∑∑(Xij*Rj)
CONSTRAINTS:
Xij int, 1<=i<=12, 1<= j <=3 决策模型和分析代考
(Xi1*1 +Xi2 *2 + Xi3*3) <= 8, for each i=1,2,3,…12
(Xi1*2 +Xi2 *4 + Xi3*7) <= 188, for each i=1,2,3,…12
Xij <= Rij, for each i=1,2,3,…12, j =1,2,3
#R: requested number of projects
See Bonus Question Below!!!
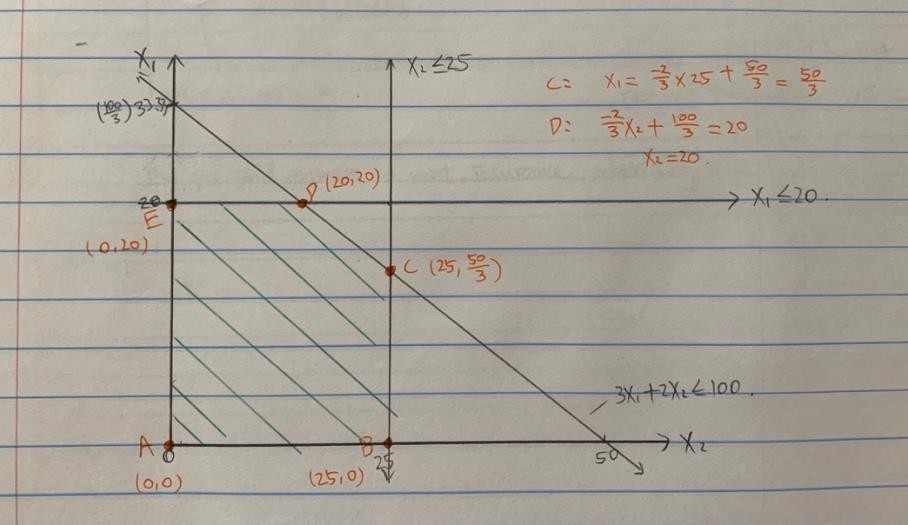
Bonus Question 决策模型和分析代考
Maximize 4X1 + 2X2 Constraints:
X1 ≤ 20
X2 ≤ 25
X1 ≤ -2/3X2 + 100/3 X1, X2 ≥ 0
Values:
A: 2(0) + 4(0) = 0
B: 2(25) + 4(0) = 50
C: 2(25) + 4(50/3) = 350/3 = 116.67 D: 2(20) + 4(20) = 120
E: 2(0) + 4(20) = 80
-We cannot go from point D to point E because the value would decrease.
-Therefore, D is the optimal point with optimal value of 120.
-The oracle is right because (20, 20) is the optimal solution with optimal value of 120.