Math Models of Operations Research, MATP 4700.
Second Exam, Tuesday, November 6, 2018.
运筹学代写 You may use any result from your notes or a homework that is clearly stated. You mayuse one sheet of handwritten notes, but no other sources.
You may use any result from your notes or a homework that is clearly stated. You mayuse one sheet of handwritten notes, but no other sources. The exam consists of five questions, and lasts one hundred and ten minutes.
| Q1 | / 20 |
| Q2 | / 20 |
| Q3 | / 25 |
| Q4 | / 15 运筹学代写 |
| Q5 | / 20 |
| Total | / 100 |
| Grade |
1.(20points) For any m × n matrix A, consider the following statement: either the system Ax > 0 has a solution, 运筹学代写
or the system AT y = 0, y 0, y = 0 has a solution,
but not both systems have solutions.
(a)(10points) Write down a linear program that will determine whether or not the second system has a solution.
(b)(10points) What is the dual of the linear program in part (1a)?
2.(20points) The canonical form tableau for the following linear optimization problem is in optimal form: 运筹学代写
minx∈R3 12x1 + 30x3
subject to 3x1 + x2 + 6x3 = 12
x1, x2, x3 ≥ 0
The optimal solution is x∗2 = 12, x∗1 = x∗3 = 0. It has been determined that we need to add the additional constraint x2 ≤ 6, giving a modified primal problem.
(a)(10points) Add the constraint to the problem and solve the problem using dual simplex. (You should only need one ) 运筹学代写
(b)(5 points) What is the dual problem to the modified primalproblem?
(c)(5points) What are the initial and final dual iterates?

3.(25 points) Consider the linear optimizationproblem 运筹学代写
minx∈R2 8x1 + 3x2
subject to x1 + x2 ≥ 6 (P )
3x1 − 2x2 ≥ −12
x1, x2 ≥ 0
(a)(5points) With the signs of the inequalities omitted, the dual problem to (P) can be written
maxy∈R2 6y1 − 12y2
subject to y1 + 3y2 ?? 8 (D)
y1 − 2y2 ?? 3
y1, y2 ?? 0
Give the dual problem including the signs of the inequalities.
(b)(10points) The point x∗ = (0, 6) is optimal for (P). Use complementary slackness to show that the dual problem has multiple optimal Give two different dual optimal solutions.
(c)(10points) Graph the dual problem and show the set of dual optimal solutions.
4.(15points) A feasible solution x is given to the following minimum cost network flow problem with capacities: 运筹学代写
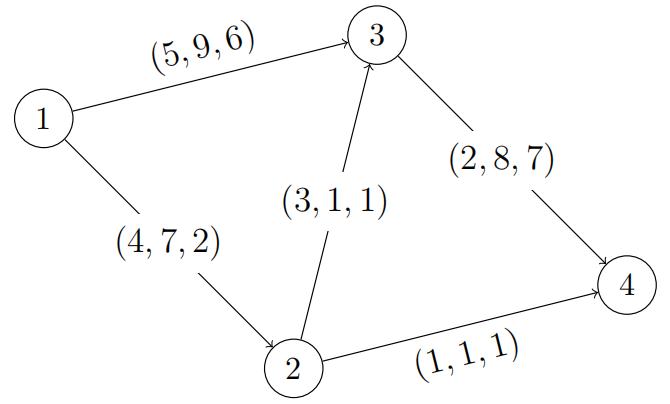
Node 1: Supply 8
Nodes 2, 3: Transshipment
Node 4: Demand 8
edge labels:
(cost cij, capacity uij, flow xij) 运筹学代写
The given solution is a basic feasible solution, with basic variables x12 = 2, x13 = 6,
x34 = 7, and nonbasic variables both at their upper bounds: x23 = 1, x24 = 1.
Solve the problem using the network flow simplex algorithm. (You should be able to solve the problem in one iteration. Be sure to show that your solution is optimal.)
5.(20points)
(a)(10points) An optimal solution to the following uncapacitated network flow prob- lem is indicated:
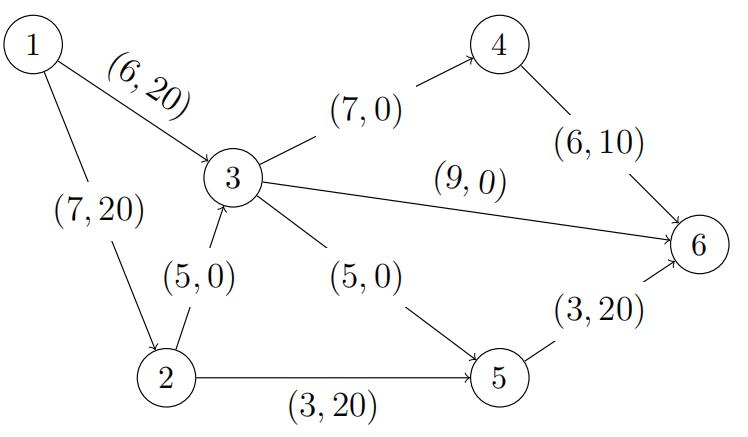
Node 1: Supply 20
Nodes 2, 3, 5: Transshipment
Node 4: Supply 10
Node 6: Demand 30
edge labels:
(cost cij, flow xij) 运筹学代写
The edges in the optimal basis are (1, 2), (2, 5), (3, 5), (4, 6), (5, 6). The optimal dual solution is y1 = 13, y2 = 6, y3 = 8, y4 = 6, y5 = 3, y6 = 0. We are considering adding an edge (1, 4). What must the cost c14 be for it to be attractive to use this edge?
(b)(10points) In a transportation problem with more demand than supply, a dummy supply node is Optimal primal and dual solutions are given in the following transportation tableau, where the first supply node is the dummy one:
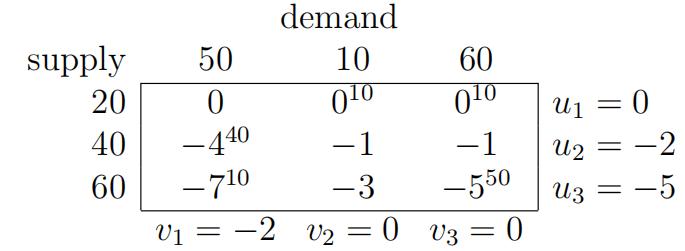
(Note that the cost of each edge is negative, since this is a revenue maximization problem written as an equivalent mimimization problem.)
Assume extra supply ∆ can be purchased at source 2. How much would you be willing to pay per unit of additional supply? What is the maximum amount you would purchase at this price? Where is the decrease in unmet demand? What is the modified shipping schedule?

更多代写:大数据代写 留学生网课考试代考 留学作业Goal Essay代写 伦敦essay代写 论文代写term paper 北美留学生report报告写作
