STA365 Assignment 1
数学模型建模代写 Assignment instructions and marking information:The assignment should be produced using RMarkdown, R, and Stan. Each task is worth 10%
Assignment instructions and marking information
The assignment should be produced using RMarkdown, R, and Stan.
- Each task is worth 10%
- All code for performing each task must be present. If there is no code you will lose most marks.
- Each task requires some reflflective writing. Make sure you write things! In particular, there is no single solution to this task, so the justifification and interpretation of the steps is important! Two otherwise identical solutions with difffferent justififications and interpretations could receive very difffferent marks.
- Each task requires the production of several plots and fifigures. These plots should be cleanly laid out with adequate captions, markings, labels, and legends.
This is an assignment that uses real data and a real mathematical model. As such, you should be prepared for the model to possibly be a poor fifit for the data. You will also most likely get some warnings in your Stan code during the warmup phase. This is ok and don’t worry about them! There may be very occasional warnings during the sampling phase, and you should become increasingly concerned as the number of warnings in this phase increases!
Modelling the dynamics of a Chalmydia infection 数学模型建模代写
Chlamydia trachomatis, an obligate intracellular bacterial pathogen that infects the genital and ocular mucosa of humans causing sexually transmitted disease and trachoma, is the most common bacterial sexually transmitted disease in humans. Women face the most serious consequences of the infection including chronic pain, tubal factor infertility, ectopic pregnancy, and pelvic inflflammatory disease resulting from genital tract infections. In a majority of cases, the infections are asymptomatic and may persist for months to years without treatment or diagnosis. Such outcomes contribute to C. trachomatis being positioned as the most costly sexually transmitted infection besides HIV/AIDS with the health care costs in the United States alone rising to at least $2 billion per year. 数学模型建模代写
C. trachomatis is an intracellular pathogen
That replicates via a unique biphasic developmental cycle involving eukaryotic cells and two distinctive forms of the bacteria: the Elementary Body (EB), which is the extracellular, metabolically inert, infectious form; and the Reticulate Body (RB), which is the intracellular, replicating structure. In this developmental cycle (see the diagram), the infectious but metabolically inactive elementary body, approximately 0.3 µm in diameter, is endocytosed by eukaryotic cells and resides within a cytoplasmic inclusion. Within the inclusion, the EBs transform into the non-infectious, but metabolically active and larger (approximately 1 µm in diameter) reticulate body. The RBs replicate via repeated cycles of binary fifission, before difffferentiating back to the infectious EB form. The EBs are then released to the cell exterior upon cell lysis¹.
¹ In less technical language, the EB invades the cell and lives within it. It then transfroms to an RB and these RBs reproduce, before turning back into EBs and exploding out of the cell (in the lysis event). This is approximately the plot of the fifilm Alien.
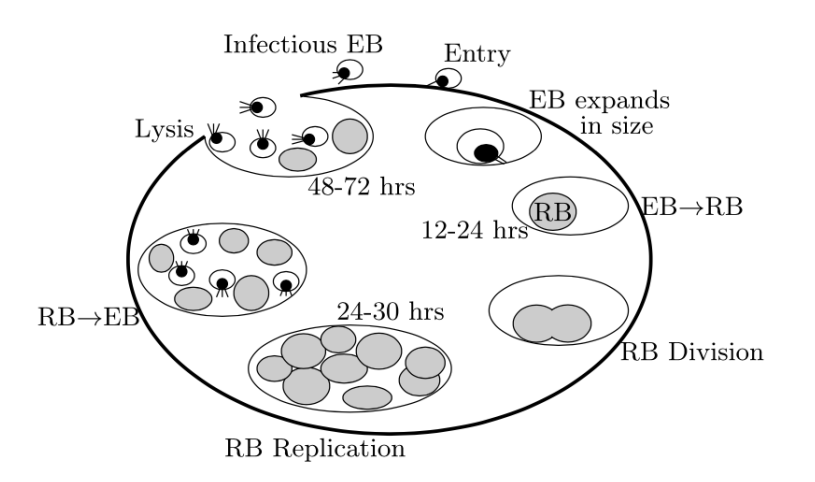
Figure 1: A diagramatic representation of the life-cycle of Chlamydia. Taken from Mallett et al., Bull Math
Biol (2013) 75:2257–2270.
The data 数学模型建模代写
Our data has been digitally extracted from Figure 1 in Rank et al. (2003)² , which measures the number of EBs in a female guinea pig’s genital tract over time. This data is measured once every 3 days after infection (days 3–30). In all cases, the infections had completely cleared within 21 days.
The data from Rank et al. (2003) was collected in two waves. Firstly, the female guinea pigs were artifificially infected with a known number of EBs (ranging from 10–10000). The number of EBs in their genital tract was then measured every day and the results report the average number across all infected guinea pigs that received the same dose. This will be the data used in Task 2
In the second wave of data, male guinea pigs were infected and the infection was passed sexually to female guinea pigs. One of the aims of the study was to understand how many EBs are passed through sexual intercourse. This will be the data used in Task 3.
In both cases the units of the data are “104 EBs”. That is a measurement of C(t) = 1 means there are 104 EBs at time t.
² Rank, R. G., Bowlin, A. K., Reed, R. L., & Darville, T. (2003). Characterization of chlamydial genital infection resulting from sexual transmission from male to female guinea pigs and determination of infectious dose. Infect. Immun., 71(11), 6148–6154.
The mathematical model
This is a complex infection, but the dynamics of it can be modelled using a set of three ordinary difffferential equations, taken from Wilson (2004)³ . This model was proposed independently of the data based on mathematical and biological considerations. It is possible that this model may not be very good!
³ P. Wilson Mathematical modelling of Chlamydia, ANZIAM J. 45 (E) ppC201–214, 2004.

Task 1: Exploring the model and setting priors 数学模型建模代写
The data will be given counts of C(t) divided by 104 for stability. The data will be given every 3 days from infection (day 3–30). The fifirst task is to see if you can put priors on the parameters. This task is made somewhat diffiffifficult by some of the parameters having difffferent scales from others.
Make and justififiy some priors on the difffferential equation parameters (excluding PE and δE) that satisfy the following:
- The infection should be almost cleared (C(t) < 0.1) by t = 30
- The distribution of maximum values of C(t) should cover the value M, where M = 100 − −250 as C(0) = 0.001 − −1.
It may help you to know that we’d expect each lysis event to produce 100s or more cells.
It may also help you to know that the following parameters give a range of approximately [0.1, 177] for C(t) when C(0) = 0.1:
parameters <- list( P = 1000 , kappa1 = 0.1 / 1e-4, kappa2 = 0.8, Pe = 40* 1e-4 , delta = 2, gamma = 1.2, mu = 1.2 )
The package deSolve may be useful for solving difffferential equaitons in R (although you’re welcome to use any other pacakge, including just doing it in Stan).
4 The ×10−4 scaling on PE is due to the data being divided by 104 . The opposite scaling will be required for κ1.
Task 2: Fit the data (the experimental conditions) 数学模型建模代写
Fit the data to the fifirst 4 curves, where the experimental initial doses of 10–104 were used using the priors you found in the fifirst part. You will need to be careful with the prior on the observation noise, as it is common in problems like this to have an area of the posterior where the solutions are constant and the observation noise is high. You should also note that the data is an average of measurements among difffferent sized groups. Your model should reflflect this.
Comment on how well the model fifits the data. Look for prior/posterior conflflicts and examine the posterior predictive checks. If necessary, note how you should revise your prior information in light of these checks and, if necessary, make those revisions. Continue this process until you have a model that you think is fully justififiable.
Note: This is real data and, as such, there is no guarantee that this model will fifit it particularly well.
Task 3: How many EBs are passed sexually. 数学模型建模代写
One of the major aims of Rank et al. (2003) was to quantify how many Chlamydia EBs were passed into the vaginal canal through sexual intercourse with an infected male guinea pig. If we know all of the parameters of the ODE model, this becomes a problem of identifying an initial condition, that is, our unknown is C(0).
It turns out to be quite diffiffifficult to estimate this at the same time as all of the parameters, but there is another way to do it: fifind a posterior for C(0) conditional on all of the other parameters. Unfortunately, we do not know the population values for the parameters, but we we have a posterior for them. This allows us to average the conditional posterior p(C(0) | y, P, κ1, κ2, γ, µ, σ) over the joint posterior p(P, κ1, κ2, γ, µ, σ | y).
This idea is an example of multiple imputation and is described in the following algorithm:
- Sample 1 draw from the posterior distribution found in Part 1.
- Conditional on those parameter values, generate 100 samples from the posterior (use the options iter_warmup = 1000 and iter_sampling=200 in the $sample() function)
- Save one of the samples at random as the draw corresponding to the paramter values chosen in step 1.
- Repeat steps 1–3 until you have 100 samples.
Comment on the distribution of C(0) and critically assess whether or not you think this procedure has lead to a reasonable estimate of the number of EBs transmitted during sexual intercourse. You should include at least 1 reason for and against the method (or 2 reasons that are both positive or both negative if you do not believe there are any negative or positive parts to this procedure).
Give your opinion on the following quote from Rank et al. (2003):
Based on the comparison of the infection kinetics, the length of the incubation period, and the percentage of animals becoming infected upon challenge, one can conclude that the female guinea pigs were receiving approximately 10² IFU [EBs] by sexual transmission at this point in the males’ infections.

更多代写:Cs网课托管 Final exam代考价格 英国代网课 论文网课代写 英国留学生paper论文代写 选课经验代写
