MF 728: Fixed Income
Problem set # 4
固定收益代写 Swaption Pricing and Risk Management under the SABR Model: Consider the following table of normal swaption volatilities and ···
Swaption Pricing and Risk Management under the SABR Model:
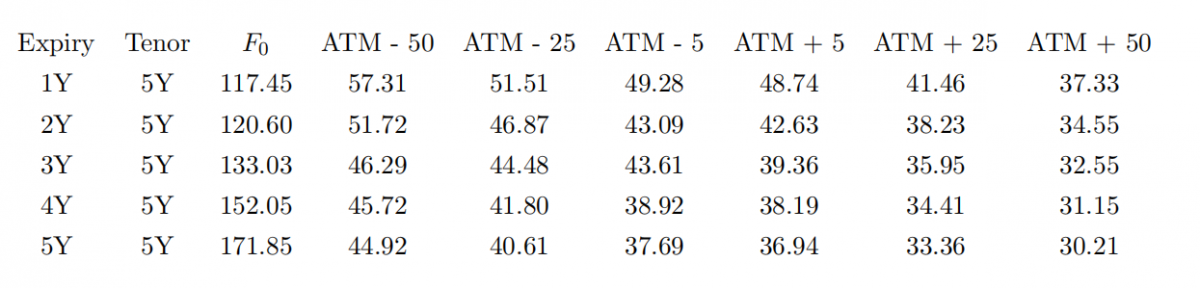
Consider the following table of normal swaption volatilities and corresponding par swap rates:
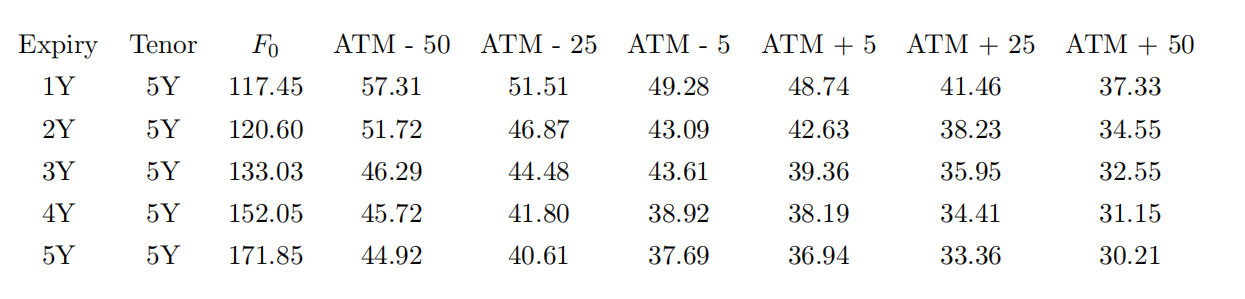
NOTE: All numbers in the table are reported in bps.
(a) 固定收益代写
Calculate the constant instantaneous forward rate for each swap that will lead to the par swap rates listed. You may use a difffferent instantaneous forward rate for each swap and are not required to go through an entire bootstrapping exercise.
(b) Using the rates obtained above, calculate the current annuity value for each swap in the above table.
(c) Calculate a table of premiums for each swaption in the table using the Bachelier pricing formula and the annuities computed above.
(d) 固定收益代写
For each option expiry, fifind the set of SABR parameters that best matches the quoted normal volatilities. Utilize the asymptotic approximation formula to calculate the normal volatility for a given set of SABR parameters and look for a solution that minimizes the distance between market and model volatilities.
(e) Comment on the relationship of the calibrated parameters as a function of expiry.
(f) Using these calibrated SABR parameters, calculate the price and normal volatility of swaptions with strikes equal to ATM – 75 and ATM + 75.
(g) 固定收益代写
Calculate the equivalent Black volatilities for each option in the table above.
(h) Calculate the delta of each options under Black’s model.
(i) Estimate a SABR smile adjusted delta for each option by calculating the expected implied shift in the volatility, σ0 for a given shift in F0. Use this to create a shift of F0 and σ0 and use this shift to approximate delta. Compare the delta you obtain using this methodology to the delta you obtained via Black’s model. Comment on any difffferences you observe.

更多代写:Jquery代写 国际关系代考 英国CS作业代写 海外Essay代写 加拿大paper论文代写 代写essay收费