Problem 1. Energy and Projectile Motion.
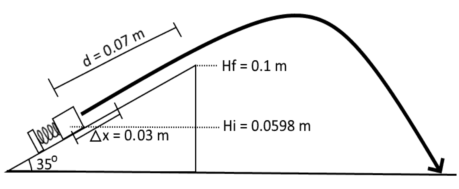
In this problem we will examine a system undergoing projectile motion using conservation of energy. Note that you must separate the kinetic energy into its x and y-components, thus the kinetic energy at any position is . The block with mass M = 6 kg is initially at rest against a spring with spring constant k = 60000 N/m. The spring is initially compressed by 0.3 m. There is no friction or air resistance and the heights at each position are shown.
- Relevant concepts/equations
- At position 1, when the block is still at rest at a height of 0.0598 m, what types of energy does the system have? What is the total energy of the block at this position?
- At position 2, when the block is at the top of the incline at a height of 0.1 m, what types of energy does the system have? What is the MAGNITUDE of the velocity of the block at his position? What is the x-velocity and y-velocity?
- After the block has left the incline it eventually reaches a maximum height. What types of energy does the block have at maximum height? What is the kinetic energy in the x-direction? What is the kinetic energy in the y-direction? What is the maximum height it attains?
5.Just before it reaches the ground (height = 0 m) what is the kinetic energy of the block? What is the final x-velocity and y-velocity of the block?
Problem 2. Torque and angular acceleration.
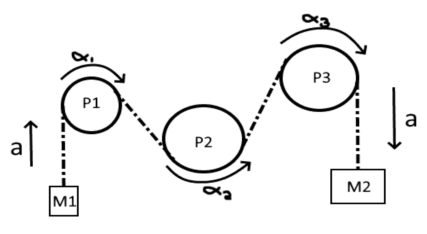
An Atwood machine consists of two masses connected by a string using three pulleys as shown. Mass M1 is 5 kg and mass M2 is 12 kg. Pulley 1 has a mass of 2 kg and a radius of 0.05 m. Pulley 2 has a mass of 3 kg and a radius of 0.08 m. Pulley 3 has a mass of 2 kg and a radius of 0.09 m. The Moment of Inertia of a pulley is .
- Relevant concepts/equations.
- Draw a Freebody diagram for each mass and a diagram of the torques for each of the pulleys
- Write the Newtonian equations for both the masses and each of the pulleys.
- What is the acceleration (tangential NOT angular) of either mass or any pulley?
- The system starts from rest. After mass 1 rises 1 meter and mass 2 falls 1 meter (and both continue to move with increasing velocity) what is the change in the total energy of the system? What is the velocity of either block (careful – energy is being used to rotate the pulleys.)
Problem 3. Inelastic collision.
A small projectile with mass m = 0.005 kg is moving toward a large block with mass M = 1.100 kg. The large mass is attached to a spring with spring constant k = 15 N/m. It rests on a surface with a coefficient of kinetic friction μk = 0.25. The small projectile is initially traveling at v = 13 m/s.
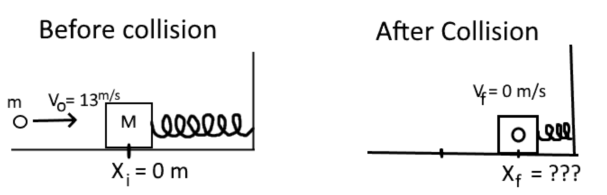
The two masses collide in a perfectly INELASTIC collision and together they are pushed to the right by a distance Xf before coming to rest.
- Relevant concepts/equations.
- What types of energy does the SYSTEM have before the collision? What is the total energy before the collision?
- After the collision the two masses are now at rest. How much work was lost due to friction? How much work was stored in the spring?
- In order for the system to be at rest the FORCE from the spring must be equal to the force of static friction. The force of static friction is F = -μsN and μsdoes not equal μk, obviously. What is the MINIMUM value of μs necessary to keep the system from moving?
- The maximum coefficient of static friction must be greater than the coefficient of kinetic friction, however you should have found the MINIMUM static friction coefficient was less than the kinetic friction coefficient. Can this be true? Explain.
Problem 4. Impulse and Momentum.
A commonly held myth is that if you were trapped in a falling elevator and you jump upward just before the elevator crashes you can escape injury. We will assume the maximum velocity a human can attain while jumping is 3 m/s upward.
Just before the elevator crashes it is traveling at 20 m/s downward. The human has a mass of 60 kg and the elevator has a mass of 1500 kg. The collision occurs over a 0.4 second interval. After the collision, the elevator and human are both at rest.
1.Relevant concepts/equations.
- What is the total initial and final momentum of the SYSTEM?
- What is the average force on the human during the collision? What is the average acceleration of the human during the collision (in units of ‘g’)?
- Was the collision survivable? A survivable collision is one for which a < 20 g. What velocity would the human have had to have to survive at a minimum acceleration of 20 g. Is this possible?
Problem 5. Angular Momentum.
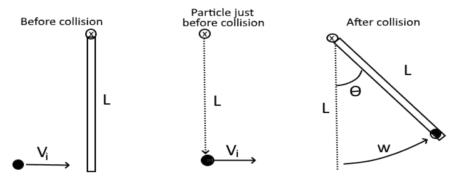
A rod with length L = 2.2 m rests on a frictionless surface. The rod has mass of M = 0.1 kg. A small projectile with mass m = 0.02 kg is traveling toward the rod at a velocity of 12 m/s. The particle strikes the rod at one end and sticks to the rod. See illustration.
1.Relevant concepts/equations.
2.The projectile may be treated as a point particle. What is the moment of inertia of the projectile? For a rod rotating about one end the moment of inertia is . What is the moment of inertia of the rod?
3.Just before the projectile strikes the rod what is the projectiles kinetic energy in terms of m and v? What is the angular velocity of the particle?
4.Just before the projectile strikes the rod what is the angular momentum of the particle? What is the angular momentum of the rod?
5.After the particle strikes the rod what is the angular velocity of the mass/rod system? How long does it take the rod to make one complete revolution?
6.If the particle had instead hit the rod at the point (3/4)L from the axis of rotation, would the angular velocity of the mass/rod system be greater or less than the value you found in part 5?
最先出自天才代写 物理代写
合作:幽灵代写
