VaR projects代写 投资组合代写

VaR projects

VaR projects代写 Consider the European digital option that pays a constant   if the stock price is above strike price X at maturity and zero otherwise.

 Section A) VaR projects代写

Consider the European digital option that pays a constant   if the stock price is above strike price X at maturity and zero otherwise. Assuming stock price   follows the following SDE under physical measure

Assuming the risk-free rate is constant t. Please write down the price of this option and explain how it is related to the price of the standard Black-Scholes European call option. 

Answer:

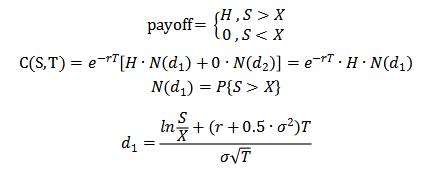
The relationship with the price of the standard Black-Scholes European call option is that they think the same way, which both calculate the payoff first, and then find the discount.

Section B) VaR projects代写

A bank has written a call option on one stock and a put option on another stock. For the first option the stock price is 50, the strike price is 51, the volatility is 28% per annum, and the time to maturity is 9 months. For the second option the stock price is 20, the strike price is 19, and the volatility is 25% per annum, and the time to maturity is 1 year. Neither stock pays a dividend. The risk-free rate is 6% per annum, and the correlation between stock price returns is 0.4.

1) Please derive an approximate linear relationship between the change in the portfolio value and the change in the underlying stocks, and then estimate the 10-day 99% VaR based on this relation.

Answer:

Because neither stock pays a dividend,

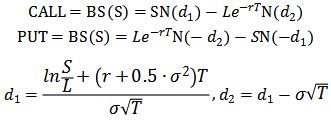
Thus,

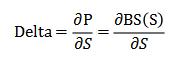
Bring into the digital,

The approximate linear relationship is,

Assume yield obeys geometric Brownian motion  VaR projects代写

Consider ten days VaR,

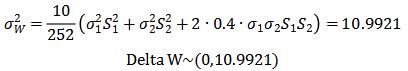
Find the quantile of order 99%, which is,

2) Using C/C++ or Java or Matlab to calculate the 10-day 99% Monte Carlo Simulation based VaR for the portfolio. Set the number of simulation to 5000.

Answer:

Step1: calculate the option portfolio value at time 0,

Portvalue0 = call0+put0 = 5.4127+1.0141;

Step2  then we use the Monte Carlo method to simulate the payoff of call option and put option according to the following relationship,

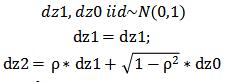
which indicates dz1 and dz2’s correlation is ρ.

then we can get the value of Euro call option and Euro put option.

Step3  Repeat step 2 for 5000 times, and we can get 5000 portfolio values. Write the option portfolio, mean we short the call option and put option. Sort to find the value of 99% of the sub-site, and the VaR is as following:

3) What else data is required to calculate the 10-day 99% Historical based VaR for the portfolio? 

Answer:

We need have the historical data on the returns or prices of this portfolio over the past time.

Matlab Code:

function [ EucallMC,EuputMC,varprice1,varprice2] = blsmc( s1,k1,T1,sigma1,s2,k2,T2,sigma2,rho,rf,ntimes)

% assume the underlying stock price can be considered to obey log normal

% distribution

nuT1 = (rf-0.5*sigma1^2)*T1;

siT1 = sigma1*sqrt(T1);

nuT2 = (rf-0.5*sigma2^2)*T2;

siT2 = sigma2*sqrt(T2);

discpayoff1 = exp(-rf*T1)*max(0,s1*exp(nuT1+siT1*randn(ntimes,1))-k1);

discpayoff2 = exp(-rf*T2)*max(0,k2-s2*exp(nuT2+siT2*(rho*randn(ntimes,1)+sqrt((1-rho^2))*randn(ntimes,1))));

[EucallMC,varprice1,ci1] =normfit(discpayoff1);

[EuputMC ,varprice2,ci2] =normfit(discpayoff2); VaR projects代写

end

clear all

clc

s1=50; k1=51; sigma1=0.28; T1=9/12;   %call

s2=20; k2=19; sigma2=0.25; T2=1;      %put

rho=0.4; rf=0.06;

siglevel = 0.99;

nsim = 5000;   %number of simulation

[call0,~] = blsprice(s1, k1, rf, T1, sigma1);

[~, put0] = blsprice(s2, k2, rf, T2, sigma2);

portvalue0=call0+put0;

portvalue = zeros(nsim,1);

for i = 1:nsim

    ntimes =100;

   [EucallMC,EuputMC,varprice1,varprice2] = blsmc( s1,k1,T1,sigma1,s2,k2,T2,sigma2,rho,rf,ntimes);

   portvalue(i)=EucallMC+EuputMC;

end

Valutatrisk=prctile(portvalue-portvalue0,siglevel*100)*sqrt(10)

其他代写：代写CS C++代写 java代写 matlab代写 web代写 作业代写 数学代写 考试助攻 paper代写 r代写 金融经济统计代写 project代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写