Stochastic Modeling代考 Midterm Exam代写

MA 583 Midterm Exam

Stochastic Modeling代考 Use fifirst-step analysis, conditioning on the possible values of X1,to show that the generating function ψn(s) solves the recursion

Instructions:

• Submit your solutions as a single PDF on learn.bu.edu.
• Solutions are due before 8:00AM on Thursday March 11, 2021.
• Explain all of your steps. YOU MUST WRITE AT LEAST ONE SEN TENCE OF EXPLANATION IN EACH STEP OF EACH PROBLEM.

• Unless stated otherwise, you need to solve any linear algebra problems by hand and you must show all of your work.

• You do not need to use a calculator. Make sure that you write any arithmetic onto your exam solutions. I will grade the arithmetic for mula as the fifinal answer, not any decimal approximation.  Stochastic Modeling代考

• You may use your notes, the textbook, and anything on the course webpage at learn.bu.edu.

• You may not use any other sources including other books or anything on the internet.
• You may not collaborate with anybody.
• Do not cheat.
• Some summation formulas are on the back page.Salins

1.(25 points) Let Xn be a Markov chain on the states {0, 1, 2, 3, 4} with the one-step transition matrix

and initial distribution

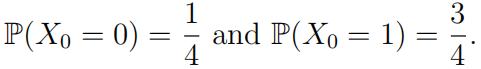
Let T = min{n : X_n ≥ 2} be the fifirst time that the Markov chain hits one of the absorbing states.

(a) Calculate P(XT = 4|X0 = 0). Show all of your work and explain each step.

(b) Calculate P(XT = 4). Show all of your work and explain each step.

2.Let ξ be a non-negative integer-valued random variable with probability generating function   Stochastic Modeling代考

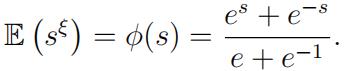
(a) Calculate the pmf for ξ. That means calculate P(ξ = k) for every integer k ∈ N. Show all of your work and explain each step.

(b) Calculate the expectation E[ξ]. Show all of your work and explain each step.

(c) Show that there exists a random variable X with generating func-tion

Hint: Random sums of random variables.

3.Let

be a transition probability matrix for a MArkov chain on the states {0, 1, 2, 3, 4}.

(a) Identify the communicating classes of the matrix. Show all of your work and explain each step.

(b) Show that µ = is an invariant distribution of P. Show all of your work and explain each step.

(c) Find an invariant distribution of the form ν =(0  0  0  a  b).Show all of your work and explain each step.

(d) Show that is an invariant distribution of P  where a and b are the numbers from part (c). Show all of your work and explain each step.

4.Let Xn be a branching process where the descendant distribution has generating function φ(s) and the initial population is X0 = 1. Let  Stochastic Modeling代考

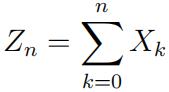
be the cumulative population size up to time n. Let ψ_n =  be the generating function of S_n.

(a) Let µ = φ’ (1). Calculate E(Z_n) for any n. Show all of your work and explain each step. For full credit, your answer should not have a summation in it.

(b) Use fifirst-step analysis, conditioning on the possible values of X1,to show that the generating function ψ_n(s) solves the recursion

ψ_n(s) = sØ(ψ_n−1(s)).

Show all of your work and explain each step.

(c) Assume that the descendant distribution has generating function

In this case, the limit

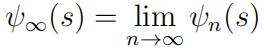
exists (You do not need to prove this claim). Use the recursion formula from part (b) to fifind ψ_∞(s). Show all of your work and explain each step.

更多代写：工程学代考  gre代考流程  国际法assignment代写  高中作业Essay代写  工程师论文代写  宏观经济作业代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写