ECE-5200 Introduction to Digital Signal Processing Autumn 2019
matlab代写 Polyphase Filter Design: There are two different approaches to the design of a polyphase inter- polation filter bank. In the “indirect”
Homework #9 Nov. 8, 2019
HOMEWORK ASSIGNMENT #9 matlab代写
Due Fri. Nov. 15, 2019 (in class)
1.Polyphase Filter Design: There are two different approaches to the design of a polyphase inter- polationfilter bank. matlab代写
In the “indirect” method, we design the “master” filter h[n] for interpolation- by-U and then downsample it to create the polyphase filters, hp[n] for p = 0, . . . , U − In the “direct” method, we individually design the U polyphase filters hp[n] to have DTFTs Hp(ejω) ≈ e−j d ω .
We can compare these two methods by examining the group delays and DTFT magnitude response of the polyphase filters, or by examining the DTFT magnitude response of the corresponding master filter. (Note that we can recover a master filter from the direct design by interleaving the polyphase filters.)matlab代写
In this problem, we will assume interpolation factor U = 15, polyphase filter length L = 11 (i.e., master filter length U L), and an input signal bandlimited to ω0 = 0.8π radians.

(a)Forthe indirect method, what are the desired passbands and stopbands of H(ejω)? Specify your answer for ω ∈ [0, π).matlab代写
(b)Derive an expression for the desired polyphase impulse response, d [n] = F−1(e−j d−p ω ).Use d = U L−1 for compatibility with the master filters designed earlier. Express your answer using sinc(x) ¾ sin(πx) , as defined in Matlab (type “help sinc”).matlab代写
(c)Usingfirls, design a causal, length-U L, generalized-linear-phase weighted-least-squares ap- proximation to the desired h[n]. Then downsample it to create the U polyphase filters hp[n].
Finally, plot matlab代写
i.The resulting DTFT magnitude response in dB versus “matlab normalized frequency”ω/π ∈ [0, 1]. Use “axis” to zoom into the range between -70 and +30 dB.
ii.Thepolyphase filters’ DTFT magnitude responses in dB versus ω/π ∈ [0, 1]. Use “axis” to zoom into the range between -0.5 and +0.5 dB.
iii.Thepolyphase filters’ group delays (use “grpdelay”). Use “axis” to zoom into the delay range between 4 and 6.
Use a total of three plots.matlab代写
(d)Designan equiripple approximation to desired h[n] via firpm and give the same plots as (c).
(e)Usethe (Hamming) window design method to directly design each of the length-L polyphase filters hp[n]. (To do this, simply multiply dp[n] from (b) by the length-L Hamming ) Next, interleave the polyphase filters hp[n] into a corresponding master filter h[n]. Finally, give the same plots as (c) and (d).matlab代写
(f)Basedon your plots, which approach do you expect to yield the best interpolator?
2.Polyphase Interpolation: We will now implement a polyphase filterbank in MATLAB using the filters designed in Problem 1.matlab代写
(a)First, generate a length-1050 signal x[n] bandlimited to ω0= 0.8π radians as follows:
i.Generatea random full-bandwidth signal u[n] using “rng(0); u = randn(1,1000)” and verify that it is full-bandwidth by plotting 20*log10(abs(fft(u,8192))). The command “rng(0)” resets the seed on the random number generator so that results are repeatable.matlab代写
ii.Using firls, design a length-51 lowpass filter g[n] with passband ω ∈ [0, 0.6π) and stopband ω ∈ [0.8π,π).
iii.Filterthe full-bandwidth signal u[n] using conv, and verify that the resulting signal x[n] has bandwidth ω0 by plotting 20*log10(abs(fft(x,8192))).matlab代写
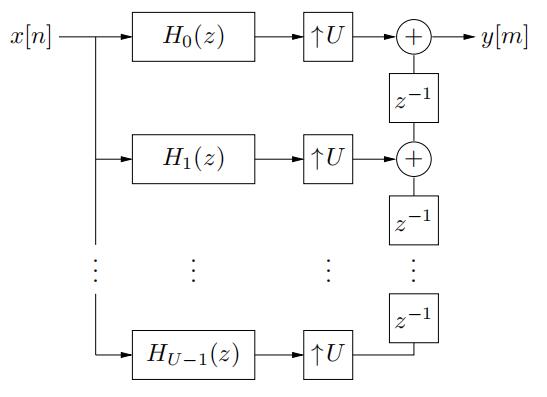
(b)Generate polyphase-interpolated y[m] using the structure below with U = 15 and the filters designed via the indirect weighted-least-squares approach from Problem 1(c). Demonstrate successfulinterpolation by plotting x[n] for n = [500 : 510] superimposed on the interpolates y[m] (for the suitable range of m).
(c)Repeat(b) for the indirect equiripple design of 1c.
(d)Repeat(b) for the direct Hamming-windowed design of 1e.
(e)Describe the performance of the interpolators. Are they consistent with your observations of the filters from Problem1?matlab代写
Hint: For debugging, recall the equivalence between polyphase and standard interpolation.

其他代写:考试助攻 计算机代写 java代写 function代写paper代写 web代写 编程代写 report代写 数学代写 algorithm代写 金融经济统计代写 finance代写 python代写 java代写 code代写 代码代写 project代写 Exercise代写 作业帮助
