Mathematical Modelling
Mathematical Modelling代写 1.(a) Derive the equation defifining the Newton-Raphson method for fifinding a root of a function f(x), x ∈ R.
1.
(a) Derive the equation defifining the Newton-Raphson method for fifinding a root of a function f(x), x ∈ R. Provide a brief explanation for each step of the derivation.
(b) Use the Newton-Raphson method with x0 = 1.0 to determine the fourth root of 2, accurate to three decimal places, showing your intermediate results.
2. Mathematical Modelling代写
Consider the initial value problem
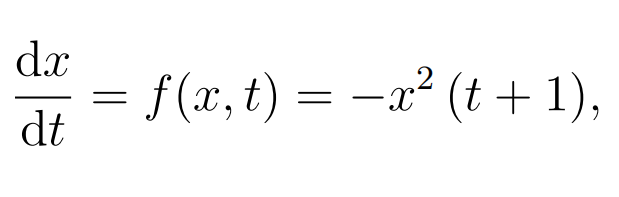
with initial conditions x = 1 for t = 0.
(a) Use Euler’s method with h = 0.1 to estimate x at t = 0.2, giving a table of appropriate intermediate steps to support your answer.
(b) Repeat the calculation in part (a) using Heun’s method. State whether you expect Euler’s or Heun’s method to be more accurate and brieflfly explain why.
(c) Obtain the exact solution of the difffferential equation (1) and compare your results from (a) and (b) with the exact solution for x at t = 0.2.
3. Mathematical Modelling代写
A one-dimensional population model is defifined by the difffferential equation
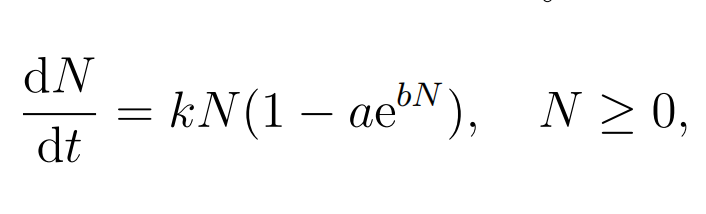
with a, b and k all positive, real parameters.
(a) Determine the conditions the parameters have to satisfy for the model to have exactly two distinct steady states, calculate these steady states, and determine their linear stability.
(b) Without solving the difffferential equation, sketch the dependence of typical solutions N(t) versus time t, including the two steady states.
4. Mathematical Modelling代写
A predator-prey model is described by the difffferential equation system
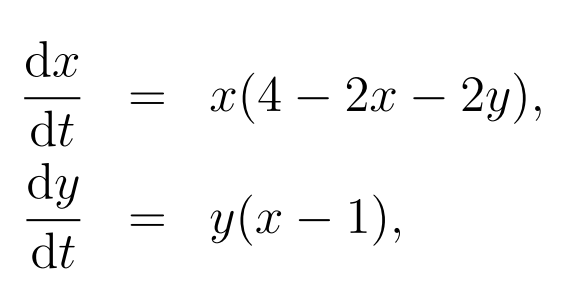
with x, y ≥ 0.
(a) Find the steady states for this system and determine the nature of each steady state.
(b) Find the nullclines of this system.
(c) Draw a sketch of the phase plane, using the information you have found in (a) and (b). To which steady state does a general initial state evolve as t → ∞?
5. Mathematical Modelling代写
A particle of mass m = 1 moves along the x-axis with velocity v i under the action of a force F(x)i, starting from x = 0 with a velocity v0 i.
(a) Using F = −dV/dx, where V (x) is the potential energy, derive the energy equation, providing intermediate steps. Identify the individual terms in the energy equation.
(b) Given that
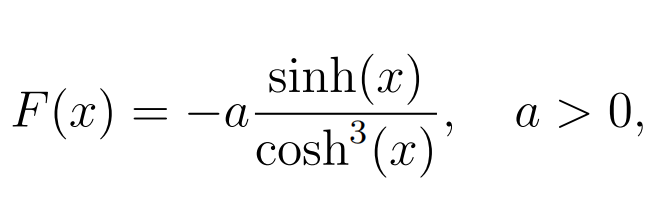
fifind and sketch V (x), under the condition that V (0) = 0.
(c) For what, if any, initial velocities v0 does the particle
(i) oscillate?
(ii) escape to +∞?
(iii) excape to −∞?
6. Mathematical Modelling代写
(a) Assume that f(x) is the periodic extension of a (square-integrable) function defifined between −l and l, such that

to derive the defifinition of the coeffiffifficient bn, giving brief explanations of your reasoning at each intermediate step.
(b) Determine the Fourier coeffiffifficients of the periodic extension of the function
f(x) = 1 − x²
defifined for x ∈ [−1, 1), providing all intermediate steps of your calculation.
Hence write down the Fourier series for f(x).
(c) Sketch the function to which the series converges for −3 < x < 3.

其他代写:作业代写 CS代写 Data Analysis代写 data代写 essay代写 英国代写 澳大利亚代写 app代写 algorithm代写 作业加急 homework代写 Exercise代写 加拿大代写 北美代写 北美作业代写 assignment代写 analysis代写 code代写 assembly代写
