Semester Two Final Examination, 2020
MATH2302 Discrete Mathematics II
MATH2302代写 a)(1 mark) Two teams (red and blue), both of size k, are chosen from a group of n (No person is selected for both teams;
1.(5 markstotal)
a)(1 mark) Two teams (red and blue), both of size k, are chosen from a group of n (No person is selected for both teams; we may assume n ≥ 2k.) State the number of such team selections in terms of k and n.
b)(4 marks) Give a combinatorial proofthat:
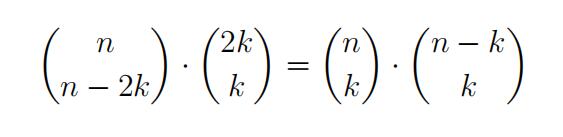
(Hint: use part (a).)

2.
(7marks total) Recall that µ : Z → {-1, 0, 1} is the M¨obius function, see the reference pages for more details. Let S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Define the poset (S, p) by
aρb if and only if a|b and µ(a) ≤ µ(b)
for all integers a and b in S. (You do not need to prove that (S, p) is a poset.)
a)(1 mark) Are 1 and 4 relatedin this poset? Explain your answer.
b)(2 marks) Find an element x in this poset such that x is both a minimal element and a maximal element. Explain your answer.
c)(4 marks) Determine the minimum number of antichains of this poset into which S can be partitioned, and justify your answer.
3.
(6 marks) Give an explicit formula for the terms of the sequence (an)n≧0whose ordinary gener- ating function is:
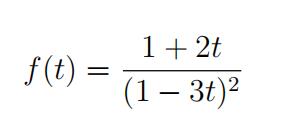
(Hint: you may have to give a separate formula for a0 and an for n ≥ 1.)
4. MATH2302代写
(6marks) Find a closed form solution for the recurrence relation
u0 = 2, u1 = 6, un+2 = 2un+1 + 3un
and prove your answer. (That is, give a formula for the general term of the sequence (un)n≧0, and justify why it is correct. Hint: you may find you are able to skip the partial fractions step.)
5.
(5 marks) Let n be an odd positive integer that is not a square. Show that the number of partitions of n into parts of consecutive sizes is an even number.
6. MATH2302代写
(5 marks total) Consider the wordba—1cd—1ee—1c—1db—1a
a)(1 mark) Draw the polygon that is represented by this word.
b)(2 marks) Compute the Euler characteristic of the corresponding surface.
c)(1 mark) Is the corresponding surface orientable or non-orientable? (No explanation re- quired.)

7. MATH2302代写
(7 marks total) For a surface S, let S′ be the connected sum of S with a Klein bottle. (So S′ = S#K where K denotes the Klein bottle.)
a)(2marks) Give a formula for x(S′) in terms of x(S). Explain your answer (you may cite a formula from class without proving it).
b)(2 marks) For what surfaces S will the resulting surface S′ be orientable? Explain your answer.

8. MATH2302代写
(6 marks total) Answer the following questions about graphs.
a)(2 marks) Decide whether the sequence 4, 4, 3, 2, 2, 2 is graphicalor Explain your answer.
b)(1mark) Show that the sequence 4, 3, 3, 2, 2, 2 is graphical by giving a graph that has this degree sequence.
c)(3 marks) What is the vertex chromatic number of the graph you specified in part (b)? Justify your answer.
9. MATH2302代写
(7 marks total) Let G be the graph constructed as follows. The vertices correspond to 2-element subsets of the set {1, 2, 3, 4, 5, 6, 7, 8} .Two vertices are adjacent if and only if the corresponding sets are disjoint.
a)(1 mark) Determine the order of G (the number ofvertices).
b)(2 marks) Determine the size of G (the number ofedges).
c)(4 marks) Show that G is Hamiltonian.
10. MATH2302代写
(5marks total) Consider the weighted graph given in the picture below.
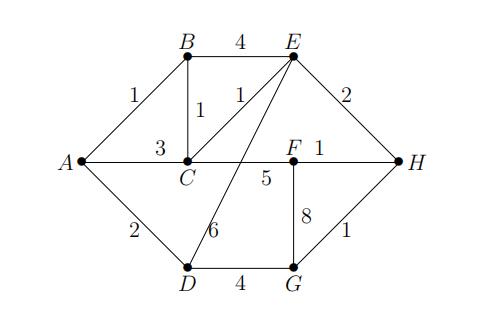
The edges of the graph have the following weights: w(A, B) = 1, w(A, C) = 3, w(A, D) = 2,w(B, C) = 1, w(B, E) = 4, w(C, E) = 1, w(C, F ) = 5, w(D, E) = 6, w(D, G) = 4, w(F, G) = 8,w(E, H) = 2, w(F, H) = 1, w(G, H) = 1. (The graph has 13 edges in total.)
a)(4marks) Use Dijkstra’s algorithm to determine the shortest distance from vertex A to each other vertex in the graph. Show each step of the algorithm.
b)(1 mark) State a shortest path from A to F in the graph.
11. MATH2302代写
- (g1, g2) 2 Ett, e. g1and g2 are connected by an edge in G, or
- (h1, h2) 2 EH, e. h1and h2 are connected by an edge in H.
a)(3 marks) Prove that if both G and H have at least one edge, then P is not a tree.
b)(3 marks) Prove that if Gor H has a perfect matching then so does P.
c)(3 marks) Prove that xV(P ) ≤ xV (G) · xV (H) (where xV denotes the vertex chromatic number).
12. MATH2302代写
(5marks total) We wish to construct a Steiner Triple System of order 25 using the Bose or the Skolem construction.
a)(2 marks) Which construction should we use? Explain your answer.
b)(2marks) Determine the number of triples in this Steiner System of order 25.
a)(1 mark) State the triple containing the points (4, 1) and (4,2).

其他代写:homework代写 Exercise代写 algorithm代写 essay代写 C++代写 C/C++代写 code代写 course代写 CS代写 assignment代写 analysis代写 app代写 assembly代写 Data Analysis代写 data代写
