MATH 2004: FINAL EXAM
MATH 2004代写 Instructions: You have 2 hours to answer all 8 questions for a total of 75 points.You must show sufficient work to justify your answer and ···
Taking this exam confirms your agreement with the following statement: I understand my responsibility to uphold and maintain Fordham University’s Code of Conduct. Any work that I claim to be my own will be my own; I will give appropriate credit where credit is due; I will be fair and honest in all of my interactions with members of the Fordham community.
Instructions: You have 2 hours to answer all 8 questions for a total of 75 points. You must show sufficient work to justify your answer and receive full credit. Points will be deducted for disorganized or untidy work. You may not use books, notes, or elec- tronic devices other than non-graphing calculators. Please scan your work and submit it via email ([email protected]) as a single pdf ftle. Have fun and GOOD LUCK!
1.(10points) MATH 2004代写
Let L be the line given by r(t) = 1, 2, 3 + t 3, 2, 1 and let P (1, 2, 1) be a point.
a)Findthe equation of the plane containing the point P and the line L.
b)Computethe area of the triangle with vertices P (1, 2, 1), Q(1, 2, 3) and R(4, 4, 4).
2.(10 points) MATH 2004代写
Consider the function
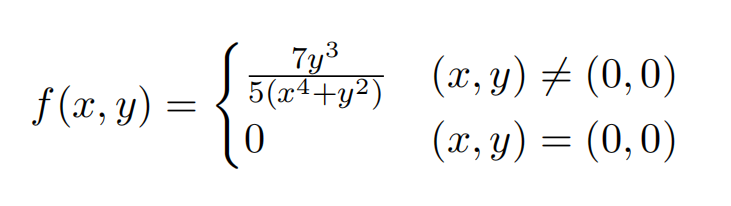
a)Showthat f (x, y) is continuous at (0, 0).
b)Computefy(0, 0) using the limit definition of the partial derivative.
3.(10points) MATH 2004代写
Recall that the arc length of a vector function r(t) from t = a to t = b
is given by
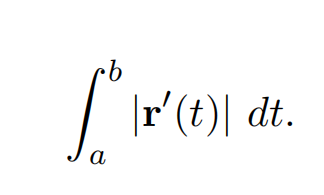
Let r(t) = e−t cos(t), e−t sin(t) .
a)Compute the arc length of r(t) from t = 0 to t =1.
b)Are there any values of t where r(t) is orthogonal to rj(t)? Explain why or why not.
4.(10points)
Let f (x, y) = x2 y2.
a)Compute ∇f(2, 1) and use it to find the equation of the tangent line to the level curve f (x, y) = 3 at (2, 1). Please give this line in two forms: using parametric equations and in the form ax + by = c.
b)Sketch the level curve, the tangent line, and the gradient vector computed above.
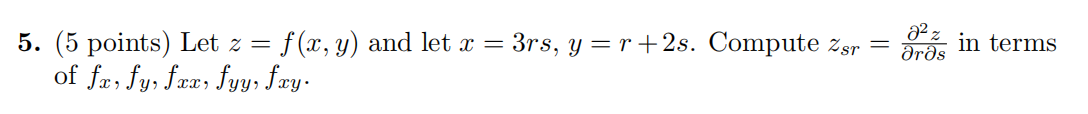
6.(10points) MATH 2004代写
Let f (x, y) = 2y2 + x4 2x2.
a)Find the critical points of f(x, y).
b)Determinethe type of each critical point.
c)Find the absolute maximum and minimum values of f (x, y) on theregion
Ω = {x2 + y2 ≤ 2}.
7.(10 points) MATH 2004代写
Let D be the region in the second quadrant of the xy-plane bounded by y = −x, x = 0 and x2 + y2 = 4.

d)Evaluate the integral using any method you wish.
8.(10points) MATH 2004代写
Let R be the triangular region in the xy-plane with vertices (0, 0), (7, 1), and (1, 7). Consider the transformation (or change of variables) given by x = 7u + v and y = u + 7v.
a)Find the region S in the uv-plane corresponding to R (the so-called “pre- image”).
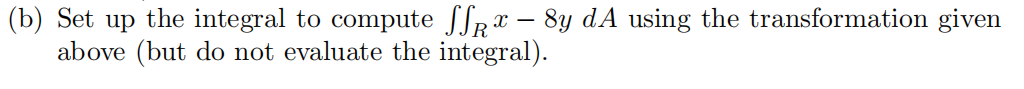

其他代写:homework代写 Exercise代写 course代写 app代写 algorithm代写 assignment代写 analysis代写 北美代写 北美作业代写 澳大利亚代写 essay代写 作业代写 作业加急 加拿大代写 英国代写 code代写 assembly代写 CS代写 Data Analysis代写 data代写
