Linear Algebra作业代写 MTH 342代写

MTH 342 OSU Spring 2022

Linear Algebra作业代写 For each eigenvalue λ, fifind at least one corresponding eigenvector. (Be sure to write the eigenvector of T as an element of M2×2.)

Thursday, May 19, Worksheet 14. Complete and submit to Gradescope by May 23.Here are some essential facts from Chapter 4 in LADW.

1. Let λ1, . . . λr be distinct eigenvalues of A ∈ Mn×n(C) and let 1, 2, . . . r be corresponding eigenvectors. Then the vectors 1, 2, . . . r are linearly indepen dent.

2. Corollary: if A ∈ Mn×n(C) has exactly n distinct eigenvalues with correspond-ing eigenvectors ~v1, ~v2, . . . ~vn then {1, 2, . . . n} is a basis of C n , and A diago-nalizable.   Linear Algebra作业代写

3. Let A be an n × n matrix. Let λ be an eigenvalue of A. Then the geometric multiplicity of λ, which is the dimension of the eigenspace ker(A − λI), is less than or equal to the algebraic multiplicity of λ.

4. A matrix A ∈ Mn×n(C) is diagonalizable if and only if for each eigenvalue λ the geometric multiplicity of λ coincides with the algebraic multiplicity of λ.Note: the process of diagonalizing A may require working with complex num-bers, even if the entries of A are real. For example, let A be the rotation matrix

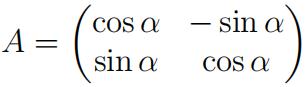
This has distinct eigenvalues e iα and e −iα, so it is diagonalizable:

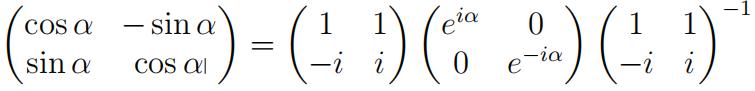
1.Let 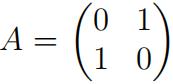. Is A diagonalizable? If it is, fifind a diagonal matrix D and an invertible matrix S such that A = SDS⁻¹.  Linear Algebra作业代写

2. Let M2×2 denote the vector space of 2 × 2 matrices with real entries. Defifine the linear transformation T : M_2×2→ M_2×2

by T(A) = A^T .

(a) Find the eigenvalues and eigenvectors of T. (Hint: while it is possible to write a matrix of this transformation in some basis, compute its characteristic polynomial and so on, it is easier to fifind eigenvalues and eigenvectors directly from the defifinition of T.)

(b) For each eigenvalue λ, fifind at least one corresponding eigenvector. (Be sure to write the eigenvector of T as an element of M_2×2.)

(c) Is it possible to diagonalize T? This means: is it possible to fifind a basis B of M_2×2 such that [T]BB is diagonal? If it is, what is B and what is [T]BB?   Linear Algebra作业代写

(d) Revisit part (b): for each eigenvalue λ of T, list k linearly independent eigen-vectors corresponding to λ, where k is the geometric multiplicity of λ.Let V be a real or complex vector space. An inner product on V is a function

(·, ·) : V × V → F

satisfying

1. (x, y) = (y, x) (conjugate symmetry);
2. (αx+βy, z) = α(x, z)+β(y, z) for all vectors x, y, z and scalars α, β (linearity);
3. (x, x) ≥ 0 for all vectors x ∈ V (non-negativity);
4. (x, x) = 0 if and only if x = 0 (non-degeneracy).

A vector space V together with an inner product on it is called an inner product space.

Given an inner product space V , we defifine a norm on V by

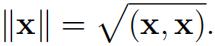
(The word norm just means length.)

3.Let x = (1, 2i, 1 + i)^T and y = (i, 2 − i, 3)^T .  Linear Algebra作业代写

(a) Compute the standard inner product (x, y) = y^∗x. Here y^∗ denotes the Her-mitian adjoint of y (the complex conjugate of the transpose of y).

(b) Compute ||x|| ² , || y|| ² , and ||y|| .

(c) Compute (3x, 2iy) and (2x, ix + 2y) without actually computing all vectors involved. This can be done using part (a) and the properties of inner product.

4.Explain why the following is not an inner product on R2:

(x, y) = x1y1 − x2y2.

Here x = (x1, x2)^T and y = (y1, y2)^T.

 

更多代写：北美英文作业代写  托福保分  大学社会心理学代写  代写Essay价格  法律论文代写  线性代数作业代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写