IEOR 3609代写 Midterm代写高级优化代写

Midterm: IEOR 3609

IEOR 3609代写 Submission Instructions.The exam contains fifive problems. (Total = 100 points). Exam duration: 2 hours. Your exam should have 5 pages.

Please read the following instructions carefully before beginning your exam.

Submission Instructions.

The exam contains fifive problems. (Total = 100 points). Exam duration: 2 hours. Your exam should have 5 pages.
Please write your name and UNI clearly on the fifirst page of your submission. Also, please write your UNI on top of every page of your submission.
You do not need to print or copy the questions in your submission. Just submit your solutions, with clearly marked problem numbers.
Submit on gradescope. Please take a clear photo or scan of your exam and upload it on the gradescope within 15 minutes of exam close time (i.e., by 10:15pm EST). The upload process is similar to homework submission. If you are having diffiffifficulty accessing gradescope, email a copy to the instructor and TA with subject line ”IEOR 3609 midterm” in order to timestamp it.

Problem 1. (20 points) IEOR 3609代写

You are given a dataset with m tuples of form (a_i, b_i), i = 1, …, m, where vector a_i∈ Rⁿ represents feature of candidate i and b_i ∈ {−1, 1} is the label for candidate i. Here label b_i = 1 means that the candidate i is qualifified for the job and b_i = −1 means that the candidate i is unqualifified.

Your task is to fifind a w ∈ Rⁿ such that the scores w^T a_i , i = 1, ..n provide a ”good” prediction of candidate qualififications in the sense that the number of candidate pairs i, j where an unqualifified candidate i received a score above a qualifified candidate j is minimized. More precisely, let B⁺ ⊆ {1, . . . , m} denote the set of qualifified candidates (those with b_i = 1), and B^– denote the remaining set of unqualifified candidates; then the goal is to fifind w ∈ Rⁿ to minimize

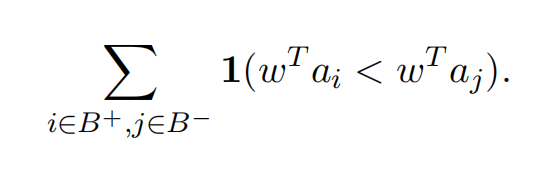
( Here 1(·) is the indicator function: 1(w^T a_i < w^T a_j) = 1 if w^T a_i < w^T a_j , and 0 if w^Ta_i ≥ w^T a_j .)

Formulate this problem as a (mixed) Integer Program.

Further clarifying remarks: The optimization problem can be written as

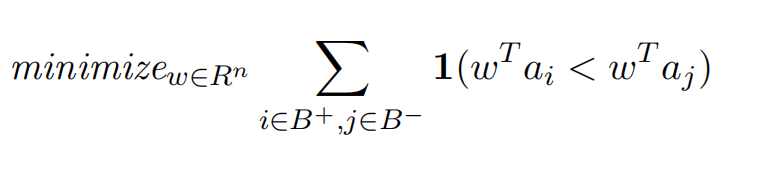
but this is not a Linear program or Integer Program since the function 1(w^T a_i < w^T a_j ) is not linear in w. There will be no credit for writing it in the above form. Your task is to use auxiliary variables, possibly binary or integer, to reformulate this optimization problem as a (mixed) Integer program.

Also note that B⁺, B^– are fifixed sets input to the program. You can use them to write constraints of form ”for all i ∈ B⁺”, ”for all j ∈ B^–” etc.

Problem 2. (20 points) IEOR 3609代写

You have received m requests for an appointment for vaccination. Each request j includes a start date s_j . Person j can receive the vaccination on any date after (and including) the start date s_j . There are 20 appointment slots for vaccination available everyday at the JK hospital. At most one request can be scheduled for one appointment slot. If a request j is scheduled for a date t_j > s_j , then we say that the request j was delayed by t_j − s_j days. (t_j − s_j is the number of days between date t_j and s_j ). Your goal is to schedule appointments such that the maximum delay over all requests is minimized.

Consider the following greedy algorithm for scheduling appointments. Order the requests in as-cending order of start dates. Then, starting from day 1, on each day schedule as many remaining requests as possible prioritized by start dates. Is this algorithm correct? If correct, give a proof of correctness. If incorrect, give a counter example.

Problem 3. (20 points) IEOR 3609代写

Consider the following integer program.

maximize z = 11x₁+ 13x₂
s.t.
x₁ + x₂ ≤ 5
4x₁ + 7x₂ ≤ 28
x₁ ≥ 0
x₂ ≥ 0
x₁, x₂ integer

Following is a partial branch and bound tree for this program.

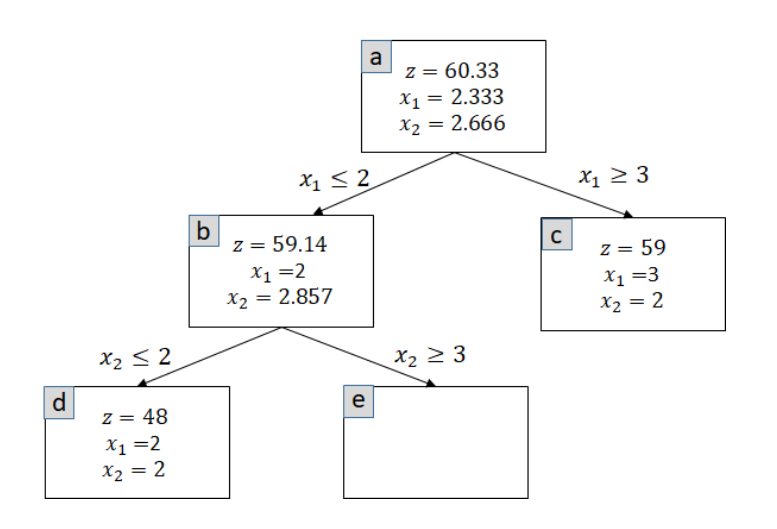
(a) (15 points)

Using the information given in the above tree answer the following.

What is the current best (highest) lower bound on the optimal solution?
What is the best (lowest) upper bound available for the value of any integer solutions obtainable from node e or its children?
Which of the remaining branches can be eliminated to prune the tree and which cannot be? Justify. You can use the letters (a,b,c,d,e) on the top left corner to refer to a node.

(b) (5 points)

Finish executing the branch and bound to fifind the optimal integer solution. You can solve any LPs using graphical method or by inspection (show your work as much as possible). Make sure to prune the tree when possible.

Problem 4. (20 points) IEOR 3609代写

Consider the following integer program.

maximize z = 5x₁ + 8x₂
s.t. x₁ + x₂ ≤ 6
5x₁ + 9x₂ ≤ 45
x₁≥ 0
x₂≥ 0
x₁, x₂integer

The optimal solution to the LP relaxation is (2.25, 3.75). The fifinal simplex tableau (including the slack variables) for this problem is as follows:

z +1.25s₁+0.75s₂= 41.25

x₁+2.25s₁−0.25s₂= 2.25

x₂−1.25s₁+0.25s₂= 3.75

Which of the following are valid inequalities? Justify. To justify that an inequality is valid, you can derive it using Chvatal-Gomory procedure or show graphically that it does not cut any feasible integer points. To show that an inequality is not valid, state an integer feasible point that does not satisfy the inequality.

(a) x₁+ 2s₁− s₂ ≤ 2

(b) x₂− 2s₁≤ 3

(d) 2x₁ + 3x₂ ≤ 15

Problem 5. (20 points) IEOR 3609代写

In the shortest path problem with delays, we are given a network G = (V, E), where each edge (i, j) ∈ E has a cost c_ij and a delay d_ij . The goal is to fifind a path from source s to terminal t with minimum cost such that the total delay over the path is at most D.

This problem can be formulated as the following integer program:

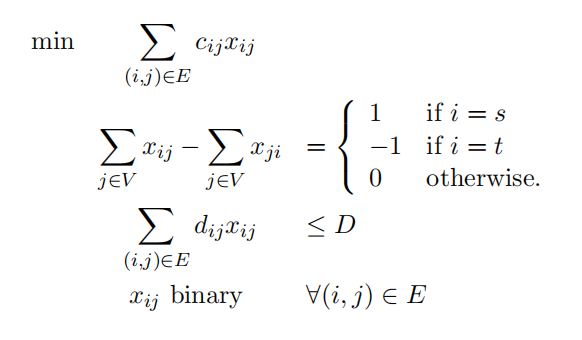
(a) (6 points)

Dualize the delay constraint (∑₍_i,j₎_∈_E d_ijx_ij ≤ D) to obtain a Lagrangian relaxation. Argue that the Lagrangian relaxation is a standard shortest path problem (with only costs and no delays) and therefore can be easily solved. State the expression for the cost of each edge (i, j) in this shortest path problem.

(b) (10 points)

Consider the following example network for the shortest path with delays problem. On each edge, the fifirst number (with dollar sign) indicates cost c_ij , and the second number (in red) indicates delay d_ij . Here source s = 1, terminal t = 6, and D = 15.

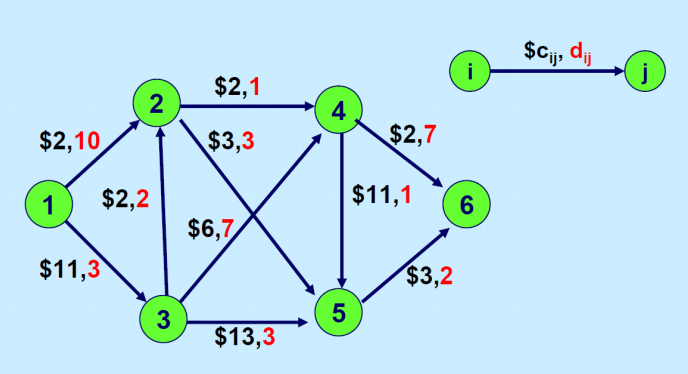
On this example network, solve the Lagrangian relaxation derived in part (a) for the following two values of the Lagrangian multiplier : µ = 0, µ = 1. You may solve the standard shortest path problem by inspection (by comparing the costs of all possible paths).

Note: If the Lagrangian relaxation you constructed in part (a) provides a lower bound only for negative values of the Lagrange multiplier, solve it for µ = 0, µ = −1.

(c) (4 points)

What is the tightest (maximum) lower bound obtained in part (b)? Is there any gap from the optimal value of the original problem? Derive an upper bound in order to bound the gap from the optimal solution. (Note that any feasible solution to the original problem gives an upper bound.)

其他代写：data代写 code代写作业加急北美代写 CS代写澳大利亚代写 essay代写 assignment代写 homework代写 report代写 paper代写加拿大代写英国代写作业代写

合作平台：essay代写论文代写写手招聘英国留学生代写