IFYFM004 Further Mathematics
Examination Exemplar
Further Mathematics代考 All working must be shown. Just giving the answer, even the correct one, will score no marks if this working is not seen.
INSTRUCTIONS TO STUDENTS
Answer ALL questions
The marks for each question are indicated in square brackets [ ].
- A formula booklet and graph paper will be provided. Further Mathematics代考
- An approved calculator may be used in the examination.
- Show ALL workings in your answer booklet.
- Examination materials must not be removed from the examination room.
DO NOT OPEN THIS QUESTION PAPER UNTIL INSTRUCTED BY THE INVIGILATOR
Question 1
The quadratic equation 3x2− 6x − 2 = 0 has roots α and β.
Without working out the values of and , find the equation with roots α3and β3.
Give your answer in the form ax2+ bx + c = 0 where a, b and c are integers.[ 4 ]
Question 2 Further Mathematics代考
Solve cosh 2x +sinh2x − 13 sinh= −3.
Give your answers in logarithmic form.[ 4 ]
Question 3
a)By differentiating a suitable number of times, obta in the Taylor expansion of
sin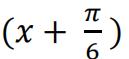 in ascending (increasing) powers of x up to the term in x2.[ 3 ]
in ascending (increasing) powers of x up to the term in x2.[ 3 ]
b)Use your result in part a) to find an approximate value of sin 36° giving your answer in terms of π.
Question 4 Further Mathematics代考
a)If (a + 3i)(b − i) = 31 + 17i, find the possible values of a and b.[ 5 ]
b)The complex number w is defined as w = 9 +40i.
Find the modulus of w and the argument of w*. Give the argument of w* to 2 decimal places.
In this question, 1 mark will be given for the correct use of decimal places.[ 4 ]
Question 5
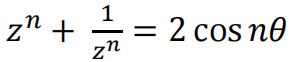
In this question you may use the results 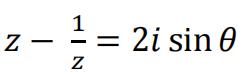 and
and
a)Expand 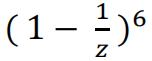 and simplify your answer.[ 2 ]
and simplify your answer.[ 2 ]
b)Hence express sin68 in the form a cos 6θ + b cos 4θ + c cos 2θ + dwhere
a, b, c and d are rational numbers. [ 3 ]
c)Hence evaluate
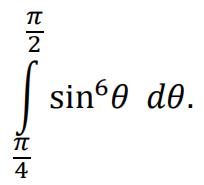
Give your answer in exact form.
All working must be shown. Just giving the answer, even the correct one, will score no marks if this working is not seen.[ 3 ]

Question 6 Further Mathematics代考
A curve has parametric equations x = √t + 1 and y = t2 − 1 (t ≥ 0)
a)Write down a Cartesian equation of the curve.
Give your answer in the form y = ƒ(x). [ 2 ]
b)Write down the equation of the normal to the curve when 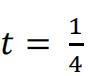 .
.
Give your answer in the form ax + by + c = 0 where a, b and c are integers. [ 3 ]
c)Integral I is definedas
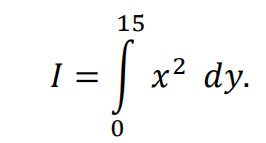
Write the integral in terms of t and hence evaluate I.
All working must be shown. Just giving the answer, even the correct one, will score no marks if this working is not seen.[ 5 ]
Question 7
An ellipse has parametric equations x = θ cos θ and y = 6 sin θ.
a)Derivethe equation of the tangent to the ellipse, and show that it can be written as 4y sin θ + 3x cos θ =24 [ 4 ]
b)The tangent crosses the x − axis at point P and the y − axis at point Q. Point M is the mid-point of PQ.
Write down the coordinates of point M in terms of θ. [ 2 ]
c)Find the Cartesian equation of the locus of point M as8 [ 2 ]
Question 8 Further Mathematics代考
In this question, all working must be shown.
a)Vectorsa and b are defined as a = 2i + 4j − 5k and b = −3i + j + =2k.
Find a × b. [ 2 ]
b)Find the coordinates of the point of intersection of the line withequation r = 3i − 4j + 2k + µ(i + 2j − 3k) and the plane which has equation (−2i + 3j − 4k) = 22.[ 3 ]
c)The position vector of a particle at time t seconds is given by
r = (−4t3 + 3t2 + 9t)i + (6t2 + 5)j + (2t + 6)k
where i, j and k are 3 mutually perpendicular vectors of length 1 metre.
Find the magnitude of the velocity of the particle when 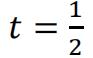 . [ 4 ]
. [ 4 ]
Question 9 Further Mathematics代考
A second order differential equation is defined as
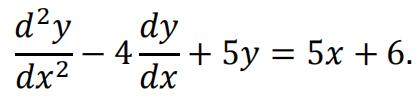
a)Find the complementary function and aparticular integral.[ 5 ]
b)Find the particular solution given y = 5 and dy= 2 when x =0. [ 4 ]
Question 10
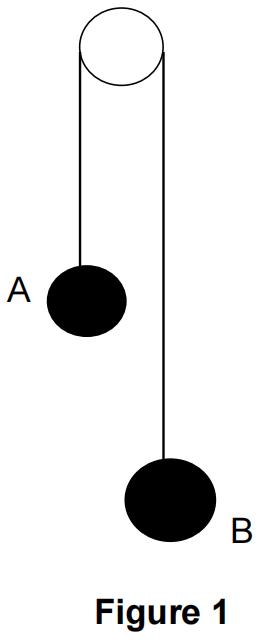
Figure 1 shows two particles A and B which are connected by a light inextensible string over a smooth pulley.
Particle A has mass M kg and particle B has mass (M + 2) kg. The system is released from rest.
Find the acceleration of the particles and the tension in the string.
Give your answers in terms of M and g, and in their simplest form. [ 5 ]
b)
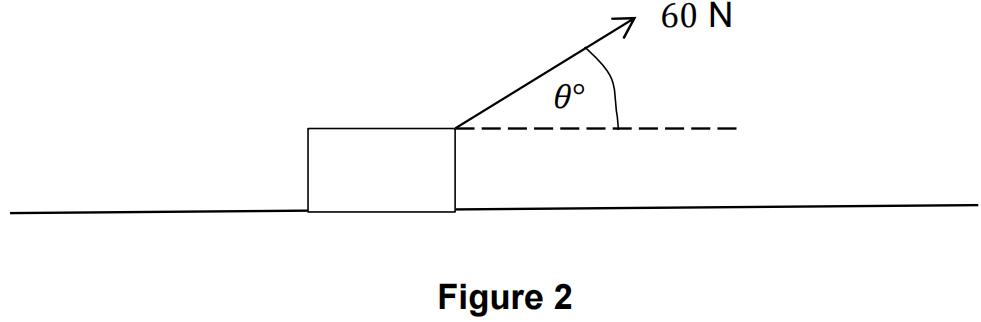
Figure 2 shows a crate of mass 20 kg being pulled along a rough horizontal surface by a rope. The tension in the rope is 60 Newtons and it is inclined at θ° to the horizontal where tan θ = ![]() .
.
The crate starts from rest and accelerates at 0.8 ms-2.
Find the coefficient of friction between the crate and the surface and how
long, in seconds, it takes the crate to travel 10 metres. [ 5 ]
Question 11

Figure 3
Figure 3 shows two spheres X and Y on a smooth horizontal surface. X has mass 4 kg and is travelling at 5 ms-1. Y has mass 6 kg and is travelling at 4 ms-1 in the same direction as X. Further Mathematics代考
The spheres collide. After the collision, both spheres continue to move in the same direction as before the collision with X travelling at u ms-1 and Y travelling at v ms-1.
The coefficient of restitution between the spheres is ![]() .
.
a)Find the value of u and the valueof v.[ 5 ]
b)Find the total kinetic energy lost in the collision.[ 2 ]
Question 12
a)Prove by induction that
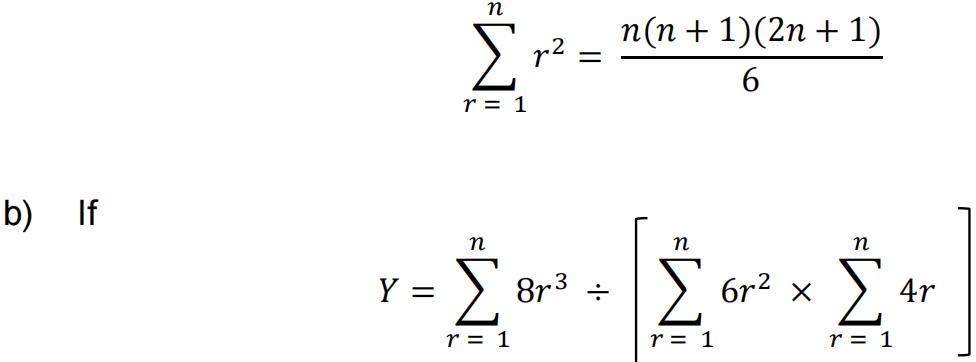
[ 5 ]
Express Y in terms of n in its simplest form, and hence find the value of n if Y = 0.008.[ 4 ]
Question 13 Further Mathematics代考
Matrix A is defined as 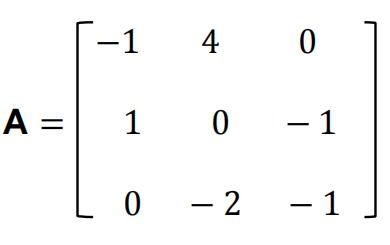
a)Find the eigenvalues ofmatrix A. [ 5 ]
b)For each eigenvalue found in part a), find acorresponding eigenvector.[ 6 ]
Question 14
a)Solve theinequality
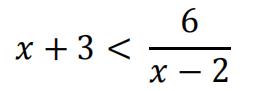
b)You are given the curve 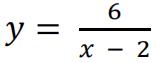 has no stationary values.
has no stationary values.
Sketch the curve 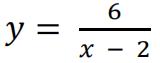 . This must not be done on graph paper.
. This must not be done on graph paper.
On your sketch, show clearly any asymptotes and the coordinates where the
curve crosses the y − axis. [ 3 ]
c)Draw and label the line y = x + 3 on your sketch.
Show clearly the coordinates where the line y = x + 3 and the
curve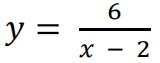 intersect. [ 2 ]
intersect. [ 2 ]
Question 15
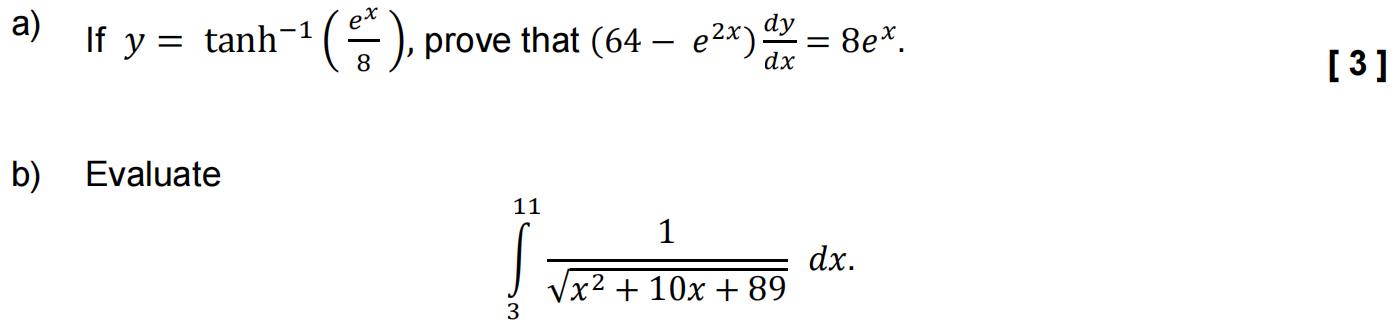
Give your answer as a single logarithm and in exact form. [ 4 ]
c)Point P lies at 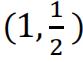 on the curve
on the curve 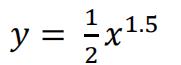
Find the length of the arc of the curve between the origin and point P.
Give your answer in the form ![]() where p and q are integers. [ 5 ]
where p and q are integers. [ 5 ]

