STATG003/M003 STATISTICAL COMPUTING
ASSESSMENT 3 (2017/18 SESSION)
Your solutions should be your own work and are to be handed in by yourself to the
Statistical Science Departmental Office by 4pm on MONDAY, 23th of April 2018.
Detailed submission instructions are given below.
Before you hand in your work, complete and sign the slip below this rubric, cut it off
and attach it firmly to your work.
When you submit your work, please make sure that someone in the Departmental
Office records on their list of students that you have handed in your work.
Late submission will incur a penalty unless there are extenuating circumstances (e.g.
medical) supported by appropriate documentation. Penalties are set out in the latest
editions of the Statistical Science Departmental Student Handbooks, available from
the departmental web pages.
Failure to submit this in-course assessment will mean that your overall examination
mark is recorded as non-complete, i.e. you will not obtain a pass for the course.
Any plagiarism or collusion will normally result in zero marks for all students in-
volved, which may also mean that your overall examination mark is recorded as
non-complete. Guidelines as to what constitutes plagiarism and collusion may be
found in the Departmental Student Handbooks. The Turn-It-In plagiarism detection
system may be used to scan your submission for evidence of plagiarism or collusion.
Your grade will be provisional until confirmed by the Statistics Examiners’ Meeting
in June 2018.
General feedback will be given via Moodle.
Declaration: I am aware of the UCL Statistical Science Department’s regulations on
plagiarism for assessed coursework. I have read the guidelines in the student handbook,
and understand what constitutes plagiarism.
I hereby affirm that the work I am submitting for this in-course assessment is entirely
my own.
Please write your name in block letters:
Your student number:
Signature:
Date:
STATG003/M003 Assessment 3 — instructions
1. You are required to write a single R function. The code for this function should
be saved in a .r file named by your student number. For example, if your student
number is 17101710, your code should be saved in the file 17101710.r .
2. Your function should be thoroughly commented. It should consist of a header
section summarising the logical structure, followed by the main body of the function.
The main body should itself contain comments.
3. You are required to submit the following:
A printout of your R script.
An electronic copy of your R script (see below).
A brief explanation of how your function works, along with a summary of its
output. The explanation should include, for example, details of any mathemat-
ical calculations that you carried out before implementing the IWLS algorithm.
Where you have made decisions regarding what to produce by way of output,
you should justify these decisions. As a rough guide, this explanation/summary
should be no more than 2 pages long.
4. Your function should not create any output files.
5. Printouts and explanations should be handed in to the Statistical Science Depart-
mental Office. Remember to complete a plagiarism declaration, and to attach it to
your work. You should ensure that all printouts are clearly identified with
your student number. Your name should only be on the cover sheet.
6. Electronic copies of your R function should be submitted via the Moodle page for the
course. Look for the link with the heading “Use this link to submit your assignment
ICA3” and follow the instructions.
STATG003/M003 Assessment 3 — R function
Suppose that Y is a vector of geometric random variables, with Yi ∼ Geo(πi) so that
P(Yi = y) = πi (1 − πi)y−1
(y = 1, 2, 3, . . .) ,
with E (Yi) = 1/πi = µi, say, and Var (Yi) = (1 − πi) /πi2. Suppose also that xi is a vector
of covariates, forming the ith row of a matrix X, such that
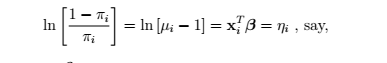
for some coefficient vector β.
This can be regarded as a GLM, since the geometric distribution is in the exponential
family and ηi is a monotonic function of µi.
Write an R function to fit such a model using iterative weighted least squares, and to
check the fitted model. Your function should be called grm (‘geometric regression model’).
The arguments to the function should be y, a vector of responses to be modelled using the
geometric distribution as described above; X, a design matrix of covariates, and startval,
an initial estimate of the model coefficients. If the user does not supply a value of startval,
you should either provide a default (e.g. a vector of zeroes or any other sensible choice) or
find some other way of starting the algorithm.
Your function should run without user intervention, and its value should be a list
object containing at least the following components (you may add more components if you
feel that these would be useful):
y: The observed responses.
fitted: The fitted values.
betahat: The estimated regression coefficients.
sebeta: The standard errors of the estimated regression coefficients.
cov.beta: The covariance matrix of the estimated regression coefficients.
p: The number of coefficients estimated in the linear predictor.
df.residual: The residual degrees of freedom.
deviance: The deviance for the model.
The structure of your function should be similar to the following:
1. Check that the dimensions of y and X are compatible, and that the data are suitable
for modelling using the geometric distribution — if not, stop with an appropriate
error message.
2. Carry out the IWLS procedure to fit the model, and output the results to screen (as
described below).
3. Produce residual plots and other appropriate model diagnostics.
4. Assemble the results into a list object, and return this as the value of the function.
In step 2, the screen output should consist of: a table showing the estimated coeffi-
cients, their standard errors, z-statistics and associated p-values; the number of coefficients
estimated; the residual degrees of freedom for the fitted model; and the deviance for the
fitted model. You may output any other relevant information if you wish.
In step 3, you should use your knowledge of model checking for GLMs to produce an
appropriate selection of diagnostics. You do not have to produce the same plots as R does
when you plot a glm object.
Your function must not use the glm command (nor anything similar such as glm.fit)!
STATG003/M003 Assessment 3 — hints
1. There is no single ‘right answer’ to this question. To obtain a good mark you need
to approach the problem sensibly, and to provide a clear justification of what you’re
doing. Credit will be given for code that is clear and readable. In particular, code
that is inadequately commented will be penalised.
2. You should ensure that your function produces output that is clearly and appropri-
ately labelled and formatted.
3. You are not required to analyse any data here; however, when marking this assess-
ment, your function will be tested on one or more datasets to ensure that it works
correctly. You may therefore wish to test your function on a simple dataset be-
fore submission, and optionally submit your test script along with your function as
described below.
4. If desired, you may use the IWLS function from Workshop 8 as a starting point for
this assessment.
5. To explain how your function works, you will probably need to use quite a lot of
mathematical notation. You are encouraged to use LATEX. That being said, a legible
handwritten explanation is also perfectly acceptable.
6. In order to explain how your function works, you will have to explain that the given
distribution is in the exponential family.
7. Your scripts will be tested by calling your function from a program that assumes that
you have done exactly what the question asks for. This means, for example, that you
must specify your function’s arguments in the order given above, and that the names
of respective elements of the list result must be the same as those given above. If
you do not do this, your function will fail when called, and you will lose marks.
8. R has some built-in routines relating to the geometric distribution. You may use
these if you think they would be useful; however, note that the definition of the
distribution in R is slightly different from that given above.
9. If you have not already done so, please read the general feedback on the first ICA on
Moodle. Also read the feedback on ICA 2 when it is made available.
10. In case you are stuck or need advice, queries regarding this assessment should be
made during an office hour. For the details of the office hours, and a link to book an
appointment, please see the Moodle page.
STATG003/M003 Assessment 3 — Optional test case
script
You are allowed to write a second script which loads a dataset, fits a regression model
using your implementation of grm, and outputs a selection of estimates and diagnostics.
The choice of data is yours, but the execution must be reproducible by any users of your
script. Hence, limit yourself to datasets which can be loaded from a R package, or which
can be constructed from R code within the script itself. For the former, we recommend the
package datasets. The choice of data and output is yours to make. The goal of this script
is for you to demonstrate to us an example of your script working in practice, in case we
have any problems running it on our own test cases. For instance, if your script works
correctly with the data provided by you but not with all of our test cases, we will be able
to give you appropriate credit for demonstrating a situation in which the script works. For
that to be possible however, we require that your test case script is clearly written and
commented. As long as the code is clear and reproducible, the format is up to you.
If you make use of this option, upload the test script as a second file. If your student
number is 17101710, say, use the format 17101710test.r .
STATG003/M003 Assessment 3 — marking guidelines
This assessment is marked out of 50. The marks are roughly subdivided into the following
components: 11 marks for correct implementation of the IWLS algorithm, 21 marks for
correct checking of input, for correct presentation of output, and for good coding style,
and 18 marks for clear explanation of how your function works, for correct diagnostics, for
correct mathematical expressions for the variance function, the deviance, etc.
代写CS&Finance|建模|代码|系统|报告|考试辅导
编程类:C++,JAVA ,数据库,WEB,Linux,Nodejs,JSP,Html,Prolog,Python,Haskell,hadoop算法,系统 机器学习
金融类:统计,计量,数据科学,风险投资,金融工程,R语言,Python语言,Matlab,建立模型,数据分析,数据处理
服务类:Lab/Assignment/Project/Course/Qzui/Midterm/Final/Exam/Test帮助代写代考辅导
E-mail:[email protected] 微信:BadGeniuscs 工作时间:无休息工作日-早上8点到凌晨3点
如果您用的手机请先保存二维码到手机里面,识别图中二维码。如果用电脑,直接掏出手机果断扫描。

