MACM 201 D100 & D200, Fall 2020
Final Exam – Part 2
December 11, 2020, 10:05am – 11:20am
final quiz代考价格 Let T = (V, E) be a rooted tree with the property that all internal vertices (all non leaf vertices) have exactly 3 children.
| Question: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
| Points: | 14 | 8 | 10 | 8 | 6 | 6 | 8 | 60 |
1.Write your answers on blank (or lined) sheets of paper. final quiz代考价格
2.You may use one page for each So you may use 7 pages in total. You may use scrap paper, but do not include that in yourupload.
3.Write your name and student number at the top of each page.
4.Foreach question, upload your answers to Crowdmark to the “box” for that question.
5.This exam is closed book – no notes, no textbook, no online resources. However, you are allowed to have up to 4 formula sheets: standard 8.5×11 inch sheets of paper (you may write on both sides).The writing must be your handwriting.

6.You may leave answers in ”calculator ready” expressions: such as10! or .15Σ25.
7.Duringthe exam, you may not communicate with another person either live, over the phone, or elec- tronically, or obtain solutions from the internet. You may not post the exam questions on chegg. Stu- dents caught cheating on the final will receive a minimum penalty of zero for the ftnal exam.
8.Examproctoring will be done using Zoom; you must be on the Zoom call with your video on while you are writing the midterm. You are required to aim your camera at your desk where you are working. We must be able to see your hands and where you are writing. During the exam you will be asked to show your face and photo ID. final quiz代考价格
9.This part of the exam will be 75 minutes long plus you will be given 10 minutes to upload your pages to Crowdmark. You must have all pages uploaded by 11:30am. The late upload penalty is 10% per minute late.
10.Before 11:20am you are not allowed to leave the camera You may not get up and go to the bathroom before11:20am.
After you have completed the actual exam, upload to Q0 of Crowdmark a picture of you holding your ID and the page containing your answer for Question 1. Your picture should look like the diagram below.
1.Short answer questions.
(a)Let G = (V, E) be a graph with 8 vertices and12 edges.How many faces can a planar embedding of G have?Justify your answer.
(b)If T is a binary tree with 5 vertices, what heights can it have?Draw an example of a binary tree for each height.
(c)The expression 2 3 4 5 + + is given in reverse Polish notation.
Convert it to standard notation.
(d)Which tree with 5 vertices has the maximumOnuffimcbiaelr toefsatrtqicuuelsattiioonn points? final quiz代考价格
Justify your answer briefly.
(e)Draw a graph with |V | = 4 that has exactly twOoffimciinailmtaelsstpqaunensintigotnrees.
Draw a graph with |V | = 4 that has exactly twOoffimciinailmtaelsstpqaunensintigotnrees.
2. Tree Traversals and Pru¨ fer Codes: final quiz代考价格
(a)Give the preorder and postorder traversals ofOthffiecrioaoltetdesttreqeubeesltoiwo.n
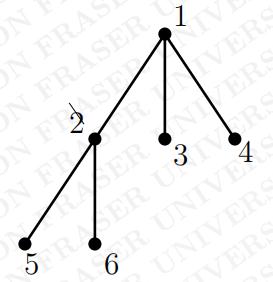
b)Give the Prufer code for the tree in part (a). Show each step of the algorithm being used.
c) Find and draw the tree which has Pr¨ufer code 2222. final quiz代考价格
3. Planar Embeddings of Graphs:
(a)Draw a planar embedding of K4 and draw itsSdIuMalO.
b)Find a nonplanar graph with 8 vertices where each vtetexquheasstdioengree 4. Explain briefly why it is non-planar.
why it is non-planar.
Find a planar graph with 8 vertices where each vertex has degress
4.Draw a planar em-bedding of your graph. final quiz代考价格
(a)For which m and n does Km,n have a HamiltonPath? Justify your answer.
(b)Consider the following true statement.
Let G be a connected graph.
If G has a vertex of degree 1 then G does not O have HteasmtiqltuonesiatnioCnycle.
(i)What is the converse of this statement? final quiz代考价格
(ii)Show that the converse is not true by giveh ga counter example.
5.Atree T has four vertices of degree 2, one vertex of degree 3,one of degree 4, one vertex of degree 5,and no vertices of higher degree. How many leaf vertices can T have? Justify your answer.
6.Let T = (V, E) be a rooted tree with the property that all internal vertices (all non leaf vertices) have exactly 3 children. If there are k internal vertices, prove, by induction on k, that |V | = 3k + 1. To receive full credit include details.
7. Consider the graph G shown below.
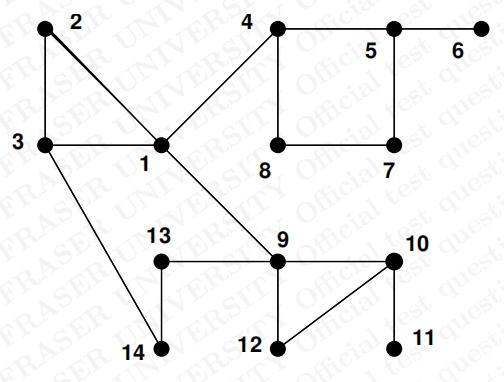
(a)List the articulation points and draw the biconnected components of G. final quiz代考价格
(b)Starting at vertex 1, draw the depth-fifirst-search spanning tree for G.
Number the edges in the order that they are visited.
(c)Now use the spanning tree you obtained from part (b) to fifind the articulation points and biconnected components in G. Use the algorithm presented in class. Show your work.

更多代写:IT assignment代写 game theory代考 英国留学生会计论文代写 留学生essay写作 英国留学生代写 History essay代写
