FIN 322
McKeever
Homework #2 – due Wednesday, November 7th, in class
FIN 322代写 a)Two risky assets, A and B, have identical return volatilities . Prove that, for any correlation , a two-asset portfolio combining A and B
1)Two-Asset Portfolio Choice (3 points each) FIN 322代写
a)Two risky assets, A and B, have identical return volatilities . Prove that, for any correlation , a two-asset portfolio combining A and B with weights and is minimally-risky when the weights are ![]() .
.
b)Two risky assets, A and B, have positive return volatilities and , with .
If , show that the weights and that would achieve a riskless portfolio are in inverse proportion to the asset volatilities ![]() .
.

2)The Efficient Frontier (3 points each) FIN 322代写
a.An investor has the utility function ![]() , where is the expected return on the portfolio and is the portfolio variance. The efficient frontier (with no risk-free asset) is given by
, where is the expected return on the portfolio and is the portfolio variance. The efficient frontier (with no risk-free asset) is given by 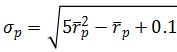 . Find the risk and expected return of the efficient portfolio that this investor will choose to maximize his or her utility. (Hint: write the investor’s utility function in terms of , then find its maximum.)FIN 322代写
. Find the risk and expected return of the efficient portfolio that this investor will choose to maximize his or her utility. (Hint: write the investor’s utility function in terms of , then find its maximum.)FIN 322代写
b)Now, let’s assume that there is a risk-free asset that returns the risk-free rate ![]() , and that the maximum Sharpe ratio of all the portfolios found on the efficient frontier is . Find the risk
, and that the maximum Sharpe ratio of all the portfolios found on the efficient frontier is . Find the risk ![]() and expected return
and expected return ![]() of the efficient portfolio
of the efficient portfolio ![]() that the same investor (utility function
that the same investor (utility function ![]() ) will choose to maximize his or her utility. Additionally, show that the investor’s utility from portfolio is greater than the utility from portfolio
) will choose to maximize his or her utility. Additionally, show that the investor’s utility from portfolio is greater than the utility from portfolio ![]() .
.
c)Find the expected return and the risk of the tangency portfolio, using the efficient frontier and the CAL from parts (a) and (b) of the question.
(Hint: recall that the tangency portfolio is the unique portfolio that lies on both the CAL and the efficient frontier.)FIN 322代写
d)Graph the efficient frontier, the CAL, and the indifference curves that correspond to the investment portfolios chosen by the investor in (a) and (b), and attach the graph to your homework. You can use the graphing calculator on desmos.com, Excel, or some other method. (Hint: for graphing the indifference curves, plug in the utility function values for each portfolio, then rearrange to get by itself on one side as the dependent variable.) Then, answer these questions:
-Dropping the risk-free asset causes the investor’s portfolio to move “down” the “hill of happiness” (i.e., they get less utility from the portfolio with no risk-free asset). Can you explain this result in the context of constrained optimization?
-What are the portfolio weights on the risk-free asset and the tangency portfolio in portfolio ? Explain the portfolio strategy in terms of borrowing or lending.
3)Portfolio Optimization in Excel (7 points) FIN 322代写
Download the file “HW2.xlsx” from Blackboard. For all problems, assume limitless borrowing and lending at the risk-free rate, and no restrictions on short-selling. The risk-free rate is 10%.
a)Create the expected return vector and the covariance matrix from the data provided (ten years’ worth of annual returns for four fictional stocks: ABC, DEF, GHI, and JKL). Use the arithmetic average of returns for expected returns. Use the COVAR command or the Covariance tool in Data Analysis to create the covariance matrix.FIN 322代写
b)Find the weights of the tangency portfolio. To do this, you’ll need to construct the summing vector and the matrix . You’ll also need to find the values of the constants A, B, and C (see class notes). Use Excel command MINVERSE to construct the inverse covariance matrix. Use Excel command MMULT to multiply the relevant vectors and matrices.FIN 322代写
c)Find the expected rate of return on the tangency portfolio and the risk of the tangency portfolio . Then, plug these in to the expression for the efficient frontier to prove that the tangency portfolio is in fact on the efficient frontier.

其他代写:代写CS C++代写 java代写 r代写 algorithm代写 金融经济统计代写 作业代写 matlab代写 web代写 app代写 作业代写 物理代写 数学代写 考试助攻
