Economics 426: Sample Midterm Examination
Economics 426代写 There are 2 pages (make sure you have all 2 pages). The exam is worth 75 points. The exam is closed-book/closed-note and ···
There are 2 pages (make sure you have all 2 pages). The exam is worth 75 points. The exam is closed-book/closed-note and you may NOT use a calculator Show your work and write legibly. Good luck!
NO CREDIT will be given for answers without an explanation.
I. Robinson Crusoe: (15 points) Economics 426代写
Suppose preferences over consumption c and leisure R are given by
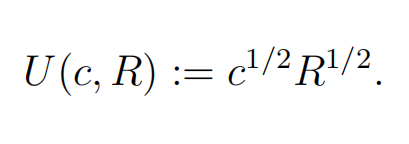
The time endowment is T = 1 and time is spent either in leisure R or working L. The consumption good is produced according to Y = F(L) := L.
A. Set up and solve the centralized problem (maximizing utility subject to feasibility). Be sure to state the optimal L*, R*and c* . (7 points)
B. Solve for the general competitive equilibrium (GCE). Be sure to explain why what you have solved for is a GCE. What is the level of profifits that the fifirm earns in equilibrium? Is the GCE Pareto optimal? Explain. (8 points)
II.Exchange Economy: (15 points)

A. Calculate the MRS for each consumer at the endowment points. Draw the Edge-worth box for this economy along with the indifffference curves for both consumers through the endowment point (one for each consumer and be clear to label which one is which). Is this endowment point Pareto effiffifficient? Explain. [5 pts]
B. Derive and graph the set of all Pareto effiffifficient allocations for this economy in the Edgeworth box (do not draw a generic curve connecting one corner to the other). Identify the contract curve in your graph. [10 pts]
III.Production in a 2x2x2 Economy: [15 points] Economics 426代写
There are two goods x and y. Good x is produced by the production function
x = f(Lₓ, Kₓ) := Lₓ + 4Kₓ,
where Lₓ is L used to produce x, Kₓ is K used to produce x. Good y is produced using a production function
y = g(Ly, Ky) := 2Ly + Ky,
where Ly is L used to produce y, Ky is K used to produce y. The total available supply of labor is L0 = 10. The total available supply of capital is Kₒ = 10.
Derive and graph the production possibility frontier, i.e., the set of (x, y) that are technically effiffifficient. You should be able to get an explicit expression for this frontier. Be sure to label any intercepts, slopes and “points of interest.” Note: the solution to your constrained optimization problem might not be interior so be careful. Hint: it might be easier to solve this problem by thinking and using a graph (as opposed to using a Lagrangean).
IV. Set Theory and Relations: [10 points] Economics 426代写
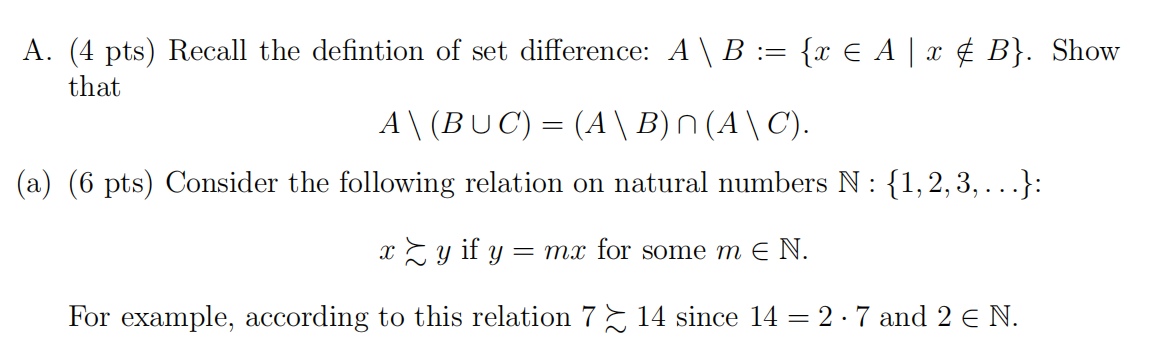
1.Is this relation reflflexive? Explain.
2.Is this relation transitive? Explain.
3.Is this relation complete? Explain.
V. Analysis (20 pts) Economics 426代写
A. (9 pts) Let A ⊂ R be given by
A := [2, 3] ∪ {1, 1/2, 1/3, 1/4, . . .}.
1.Is A closed? Explain. (1 pt)
2.Is A open? Explain. (1 pts)
3.Identify the closure of A. Explain. (1 pt)
4.Is A bounded? Explain. (1 pt)
5.Identify the interior of A. Explain. (1 pt)
6.Identify the boundary of A. Explain. (1 pt)
7.Is A compact? If not, provide an open cover of A that does not admit a fifinite subcover. (3 pts)
B. Let S ⊂ R be closed and x* be the supremum of S (i.e., least upper bound). Show that x*∈ S or provide a counterexample. [5 pts]
C. Let f : N → R with the Euclidean metric on both N and R. Show that f is continuous by showing that f -¹(A) is open in N whenever A ⊂ R is open. [6 pts]

其他代写:homework代写 加拿大代写 英国代写 作业代写 report代写 paper代写 code代写 algorithm代写 作业加急 北美代写 CS代写 Data Analysis代写 data代写 澳大利亚代写 essay代写 assignment代写 analysis代写
