投资组合管理:基于Markowitz理论和国际资产定价模型理论
你的姓名
华南理工大学广州学院 经济学院 国际经济与贸易1(2)班
指导教师 王金鹏
(说明:红色字体为操作说明,阅读后请删除,蓝色字体需要被相应内容替换)
(有关数据呈现方式:使用Excel计算的结果,通过改变单元格格式—数字—科学计数—小数位4位,代写Matlab则先将数据导入到Excel中,然后采取前述相同方法改变格式,科学计数,小数4位)
摘要:本报告分为七个部分: 第0部分为理论综述,简要介绍所需的Markowitz理论和资本资产定价模型理论;第1部分介绍数据获取途径和处理方式;第2,3部分根据Markowitz理论计算投资组合的风险收益,分别代写Excel和代写Matlab为计算工具;第4部分通过代写Matlab绘制投资组合的有效前沿;第5部分根据国际资产定价模型ICAPM估算8支股票的收益率;第6部分构建两支投资基金并且使用绩效指标进行评估
0 理论概述
- 投资组合有效前沿:
以两个资产A,B为例风险和收益分别为, , , , 两个资产间的收益率相关系数。通过改变A,B 权重,我们可以获得一系列的投资组合,其风险收益关系为如下曲线,我们定义红色区域为投资组合的有效前沿
- 资产间相关系数对组合的收益率和风险的影响
依然考虑上述资产组合,这一次假设两个资产间的相关系数分别为+1,+0.5,0,-0.5,-1,可以得到5条风险收益曲线,
风险资产与市场的组合(资本市场线CapitalMarket Line CML)
这一次将资产A替换为无风险资产其收益率和风险为,, 将B替换为市场,其收益率与风险为,, 通过构建20个组合我们得到收益率风险曲线为:
- 资产定价模型(证券市场线Security Market Line SML与特雷诺指数Treynor Ratio)
1 数据获取和股票基本信息
本文通过Wind金融客户端直接抽取如下8支股票的交易信息
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
- 证券名称,证券代码,总股本
以及上证, 深证综合指数价格
通过机构网站:
(1)美国美联储网站:美元利率汇率
(2)英国英格兰银行网站:英镑利率汇率
(3)欧洲中央银行网站:欧元利率汇率
(4)日本银行网站:日元利率汇率
(5)中国银行网站:人民币利率汇率
(6)Google Finance: FTSE 100,
(7)Google Finance: Nikkei 225,
(8)Google Finance: S&P 500
2 通过Microsoft Excel建模 (任务1:Markowitz理论计算固定组合的风险收益)
- 以上8支股票(股票名称1, 股票名称2,。。。)的平均收益率μ分别为:
(将《操作步骤》第一部分第5步结果粘贴至此)
- 收益率协方差矩阵σ(将第6步结果粘贴在单元格中)
| 股票1 | 股票2 | |||||||
| 股票1 | ||||||||
| 股票2 | ||||||||
- 8种投资品按照相同权重(总购买金额)进行组合,因此权重向量w为:
(0.125,0.125,0.125,0.125,0.125,0.125,0.125,0.125)
- 投资组合的收益率为向量乘积(此处粘贴第10步结果)
- 投资组合的风险为矩阵乘积=(此处粘贴第11步结果)
3 通过代写Matlab抽取数据并建立模型(任务2:Markowitz理论计算固定组合的风险收益)
- 股票平均收益率向量ExpR=(此处粘贴第二部第3步结果)
- 收益率协方差矩阵ExpCov=(此处粘贴第二部第4步结果,矩阵会占用多行)
- 投资组合收益率为(此处粘贴第二部第5步结果)
- 投资组合风险为(此处粘贴第二部第6步结果)
4 通过代写Matlab绘制投资组合有效前沿 (任务3:Markowitz理论求解投资组合)
- 这8只股票的投资组合有效前沿为
(此处粘贴第3部分第2步)
- 有效投资组合的权重比例为(前10组)(表格中填写第3步信息)
| 投资组合排名 | 股票名 | 股票名 | 股票名 | 股票名 | 股票名 | 股票名 | 股票名 | 股票名 |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 |
5 根据国际资本资产定价模型ICAPM估计各支股票收益率
- SRP外汇风险溢价 (5位小数)
| USD | GRP | EUR | JPY | |
| SRP |
- 证券收益率与外汇收益率的相关系数
| USD | GRP | EUR | JPY | |
| 股票(1) | ||||
| 股票(2) | ||||
| 股票(3) | ||||
| 股票(4) | ||||
| 股票(5) | ||||
| 股票(6) | ||||
| 股票(7) | ||||
| 股票(8) |
- 收益率标准差
| 证券名称 | 收益率标准差 | 外汇名称 | 收益率标准差 |
| 股票(1) | USDCNY | ||
| 股票(2) | GBPCNY | ||
| 股票(3) | EURCNY | ||
| 股票(4) | JPYCNY | ||
| 股票(5) | |||
| 股票(6) | |||
| 股票(7) | |||
| 股票(8) | |||
- 系数
| USD | GRP | EUR | JPY | |
| 股票(1) | ||||
| 股票(2) | ||||
| 股票(3) | ||||
| 股票(4) | ||||
| 股票(5) | ||||
| 股票(6) | ||||
| 股票(7) | ||||
| 股票(8) |
- 无风险收益=
- 世界市场收益=
- 世界市场风险溢价=
- 股票与世界市场的相关系数和系数
| 与世界市场相关系数 | 与世界市场系数 | |
| 股票(1) | ||
| 股票(2) | ||
| 股票(3) | ||
| 股票(4) | ||
| 股票(5) | ||
| 股票(6) | ||
| 股票(7) | ||
| 股票(8) |
- 证券收益率计算过程和结果
| 证券名称 | ||||||
6 模拟证券投资基金
本题目将考查两只投资基金,构成基金的资产为前述8只股票,业绩基准为上证(深证)指数。第一只基金为8只股票的简单组合,权重均为1/8。第二只基金的资产依然为8只股票,但是权重未知,需要通过计算获得。获得后计算两支基金的相应指标
- 以跟踪误差Tracking Error为目标函数,计算获得的权重为:(权重小数点后保留6位,如0.123456)
| 股票 | ||||||||
| 权重 |
- 两支基金与业绩基准的收益率序列对比图:(请使用你的结果替换下图)
- 两支基金的绩效对比:
简单型投资组合基金 指数追踪型基金 Sharpe Ratio Treynor Ratio Information Ratio 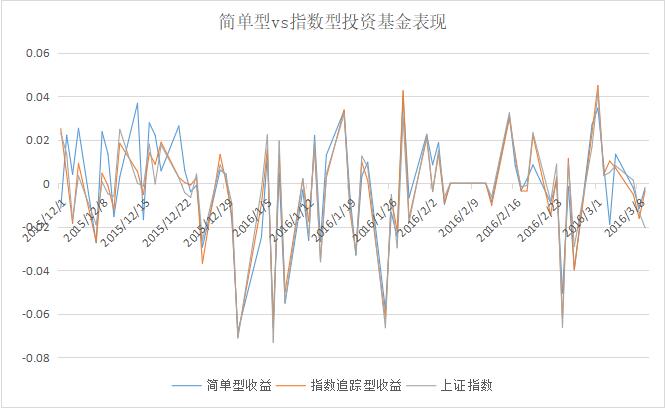
Sharp Ratio , 是投资组合(基金)的收益率均值,是无风险利率,取值1.5%,为收益率的标准差
Information Ratio , 分别代表基金的收益率序列(向量)和基准序列(即上证,深证指数)
,是基金的平均收益率,是无风险利率,取值1.5%,为投资资金对上证(深证)的系数
