CS:4350 Logic in Computer Science
CS4350代写 1.We will use propositional variables ti,j to denote that teacher i will teach course j, where 1 ≦ i ≦ 3 and 1 ≦ j ≦ 4. Please specify the ···
1.
We will use propositional variables ti,j to denote that teacher i will teach course j, where 1 ≦ i ≦ 3 and 1 ≦ j ≦ 4. Please specify the following properties in CNF using ti,j:
a. Every teacher will teach at least one course.
b. Every course must be taught by a teacher.
c. Course 4 cannot be taught together by more than two teachers.
2. CS4350代写
Using the Semantic Tableau method, show that the following formula is valid:
((A ∨ B) ∧ (A → C) ∧ (B → C)) → C
3.
We apply various resolution strategies to prove that the following clause set entails ¬ s: unit resolution, input resolution, negative resolution, positive resolution, and ordered resolution using the order of p > q > r > s.
{ p ∨ q ∨ ¬ r, p ∨ ¬ q ∨ s, ¬ p ∨ q ∨ ¬ r, ¬ p ∨ ¬ q ∨ r, ¬ p ∨ q ∨ r, ¬q ∨ ¬ r, r ∨ ¬ s }
Please show the proofs of these resolution strategies.
4. CS4350代写
Given an undirected graph G = (V, E), the graph coloring problem is to assign each vertex a color such that no two adjacent vertices receive the same color.
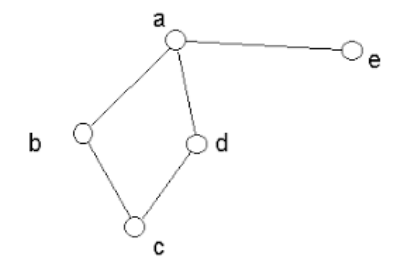
a. Specify a propositional formula A such that G = (V, E) can be colored using at most C colors iff the formula A is satisfiable.
b. Provide the details of A in (a.) if the graph is the one on the right and C = 2.
c. Provide all the models of A in (b.)
5. CS4350代写
Provide (a) minimized DNF through K-map; (b) minimized CNF through K-map; (c) complete semantic tableau; and (d) the ROBDD (assuming the order is A>B>C>D) for the following formula:
((A ⊕ B) ∨ C) → (B ∧ (C ↔ D))
6. CS4350代写
Six people sit on a bench of six seats for a group photo: two Americans (A), two Britons (B), a Canadian (C), and a Dane (D). They asked that (i) the distances from the seats taken by the Britons to the middle point of the bench are the same; (ii) either the Canadian or the Americans do not want to sit next to an American; (iii) the Dane likes to sit next to the Canadian. The photographer happily complied. Suppose we use propositional variables X,y, where X ∈ {A, B, C, D} and 1 ≤ y ≤ 6, with the meaning that “Xy is true iff the people of nationality X sits at seat y of the bench”. Please answer the following questions:
a. Specify the problem formally in CNF using X,y, such that the models of the CNF matches exactly all the solutions of the photographer.
b. What are these models in terms of X,y?
c. How to reduce the number of literals in the CNF (keep the models unchanged)?
d. Abel says to Bob and Carol: “I’ve an idea to reduce the size of the CNF: introduce some new variables. For instance, if H1 stands for “the Canadian takes seats 1, or 2, or 3” and H₂ stands for “the Canadian takes seats 4, or 5, or 6”, then clause (¬H₁ | ¬H₂) can replace clauses like (¬C₁ | ¬C₄), …, (¬C₃ | ¬C₆).” Bob says, “you introduced the new variables and changed the models of the original CNF.” Carol says, “you have to add the clauses for defining H₁ and H₂, and the CNF becomes larger instead of smaller.” Who is right and why?

其他代写:CS代写 作业代写 作业加急 homework代写 Exercise代写 essay代写 英国代写 加拿大代写 北美代写 北美作业代写 澳大利亚代写 app代写 algorithm代写 assignment代写 analysis代写 code代写 assembly代写 Data Analysis代写 data代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
