Fall 2020 CS330 Final – B
December 16, 2020
CS330代写 Problem 1 Consider an instance of the Stable Matching Problem in which one of the hospitals (call it h∗) and one of the residents (call them r∗) ···
Instructions
- Thisexam is open You may consult your textbook, notes, slides, or other course materials, but no external sources.
- Absolutelyno collaboration is allowed. You cannot discuss the contents of this exam with anyone except the instructors.
- You may reference and use anything (e.g., algorithms, proofs) discussed in lecture, labor the Outside references (i.e., anything other than your notes and the course materials) are not allowed.
- Theexam consists of 3 problems, each with several parts.
- You can write your answers by hand on paper, on a tablet, or you can type your solutions.Make sure to clearly mark the problems and also annotate with the problem number when you upload to Gradescope.
- Fromthe time you download this PDF you have 120 minutes time to upload your final pdf to There is a 10-minute grace period. If you have trouble uploading, please email your PDF immediately to [email protected].
- If you have questions, you mask them via private post on Piazza or to a course staff membervia the Zoom link posted on Piazza.
Problem 1 Short answers (19 points) CS330代写
(a) (3 points)
Consider an instance of the Stable Matching Problem in which one of the hospitals (call it h∗) and one of the residents (call them r∗) both rank each other last. Prove or disprove: this hospital and resident will never be paired together in any stable matching.
(b) (3 points)
Consider the followingrecurrence:
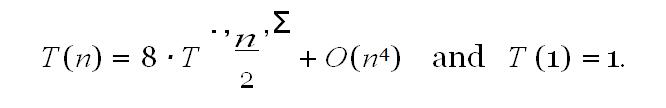
(a)Whatis the (asymptotic) depth of the corresponding recurrence tree?
(b)How many leaves does the tree have(asymptotically)?
(c)What is the solution to the recurrence (use any method you like). Justify your answer briefly (onesentence).
(c)(2points) CS330代写
Suppose we perform DFS in a connected, undirected graph. Which of the following types of edges are possible? Select all that apply:
- Treeedges
- Forward edges (i.e. from a node to one of itsdescendants)
- Backedges (i.e. from a node to one of its ancestors)
- Cross edges (i.e. from a node to a node that is neither its descendant nor its ancestor)
Whichever subset you selected, draw a connected, undirected graph in which all of them occur. Indicate the order in which DFS explores the vertices, and the type of each edge.
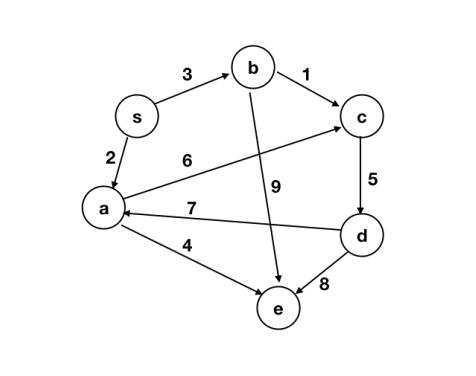
(d)(2points)
Consider the following directed Is the tree of shortest paths from s unique? If so, highlight the edges in the tree. If not, give a vertex to which there are two distinct shortest paths from s.
(e) (2points) CS330代写
Prove or disprove: Let G be an undirected graph with unique edge The minimum spanning tree of G includes the minimum-weight edge in every cycle in G.
(f) (1 points)
Suppose we have a directed graph with edge weights that may be negativeor Under what condition will there exist well-defined shortest path distances from vertex s to all other vertices (which you could then find using Bellman-Ford, for example)?
(g) (2 points)
Suppose you have a flow network G = (V, E), such that every capacity ce is an odd number. True or false: there exists a maximum flow f on G that is odd on every edge. Either prove your answer or give a counter example.
(h) (4 points) CS330代写
Consider the following two problems from class:
Max-Network-Flow (NF): On input of a graph G = (V, E, c) with integer capaci- ties for the edges, nodes s and t, and a number k, determine if there is a valid s–t flow with value at least k.
Hamiltonian-Cycle (HC): On input an undirected graph G, determine if there is a cycle that visits all vertices in the graph exactly once.
Suppose we have some problem X of unknown complexity.
For each of the following, answer Yes or No, and give a brief (one sentence) justifica- tion.
(a) Supposethere is a reduction from X to NF (that is, a polynomial-time algorithm for X that uses a hypothetical algorithm for NF as a subroutine). Can we conclude that X has a polynomial-time algorithm?
(b) Supposethere is a reduction from X to HC (that is, a polynomial-time algorithm for X that uses a hypothetical algorithm for HC as a subroutine). Can we conclude that X cannot have a polynomial-time algorithm?
Problem 2 DP (9 points) CS330代写
A bitstring A is a palindrome if the bits follow in the same order from left to right as right to left. (e.g. ’1001001’ and ’11011011’ are palindromes, while ’1011’ is not. )
Suppose that you are given a string A of bits. You can insert bits (i.e. 0 or 1) to any location in the string. However, insertions come with different costs: inserting a ’0’ costs x, while inserting a ’1’ costs y (both positive numbers).
Our goal is to compute the minimum-cost set of insertions to A so that it becomes a palindrome.
Example. Suppose A =’00010’, the cost of inserting ’0’ is 3 and inserting ’1’ costs 4. Here are two solutions of different cost, both yielding palindromes. This solution ’0001000’ (insertions in bold) costs 6, while ’010010’ costs only 4.
Here is an incomplete description of a dynamic programming algorithm InsertBits.
Read the description and answer the questions with regard to this algorithm. CS330代写
Input: array A of bits of length n, costs x and y.
Output: C, the total cost for the cheapest set of insertions that makes A a palindrome.
Algorithm description (informal): For every pair of indices i and j, the algorithm com- putes
OP T (i, j)= cost of the cheapest set of insertions that turn the substring
A[i, …, j] (consisting of the bits from index i to j inclusive) into a palindrome.
To do so, it proceeds as follows: Compare the bits at index i and j. If they are the same, we can ignore them and return the answer to a smaller subproblem (which one?). Otherwise, consider two possible solutions: one that inserts a bit at the left end of A[i, j] (and solves one subproblem), and the other that inserts a bit at the right end of A (and solves a different subproblem).
NB: Indices i and j always refer to positions in the original string (before any insertions are made). We suggest indexing from 0 to n − 1.
(a) (1 points)
What index of OP T (i, j) contains the output C? (No explanation )
(b) (5points)
Complete the recursive formula used in InsertBits. (No explanation needed.)

(c)(3points)
Here is a specific input to this problem:
x = 3 (cost to insert 0)
y = 2 (cost to insert 1)
A = [1, 0, 0, 1, 1, 0]
Compute (and write) the size n * n memoization table M , where M [i, j] corresponds to OP T (i, j). Format your answer as in the table below. (We’ve filled in the base cases where j == i and j == i − 1.)
| 0 | |||||
| 0 | 0 | ||||
| – | 0 | 0 | |||
| – | – | 0 | 0 | ||
| – | – | – | 0 | 0 | |
| – | – | – | – | 0 | 0 |
Problem 3 Traveling nurses (11 points) CS330代写
During the pandemic, traveling nurses must be sent to places where infection rates are spiking. There are P difffferent nurses practitioners, denoted by pi , and there are H difffferent hospitals that they can be assigned to. Obviously, each nurse can be assigned to at most one hospital. Each hospital hj has a demand for dj nurse practitioners. However, not every nurse is eligible to work at every hospital; for each nurse practitioner pi we know the subset si of hospitals at which they are approved to work.
Find an algorithm to decide whether there is a way to meet the demand for nurse prac-titioners at every hospital?
Your algorithm should be a reduction to network flow. Specify your algorithm by an- swering each question below. Your answer should be clear enough that any other student could turn them in to working code.
(a)(4 points) CS330代写
Design a directed graph G(V, E) that is an instance of the max-Flow problem. That is, G is directed, it has designated source s and sink t nodes and a capacityc(e) on each directed Describe each part of G:
- Specifythe vertices in G. Hint: there should be nodes for both nurse practitioners and hospitals.
- Describethe edges in G. Make clear which direction they are .
- Describe the capacity on each edge.
(b)(1points)
How many vertices does your graph have in terms of P and H (asymptot- ically)?
(c)(2points) CS330代写
What is the maximum number of edges your graph can have, in terms of P and H (asymptotically)?
(d)(2 points)
Suppose we found the maximum flow f in G. Describe how to find for eachnurse practitioner pi which hospital they are sent to based on the flow values f (e) along the edges. (Just state how to find out. No need to )
(e) (2 points)
Suppose that it is indeed possible to assign nurses so that all demands are met. In that case, what is the value of the flow that is returned by the max-flow subroutine?

其他代写:CS代写 assignment代写 homework代写 Exercise代写 C++代写 C/C++代写 essay代写 algorithm代写 analysis代写 app代写 assembly代写 code代写 course代写 Data Analysis代写 data代写
