CS 570 – HW 5
Due Friday, April 24 (by 23:30)
CS 570作业代写 1 Maximizing Profifit (10 points)A furniture company produces three types of couches. The fifirst type uses 1 foot of framing wood and ···
1 Maximizing Profifit (10 points)
A furniture company produces three types of couches. The fifirst type uses 1 foot of framing wood and 3 feet of cabinet wood. The second type uses 2 feet of framing wood and 2 feet of cabinet wood. The third type uses 2 feet of framing wood and 1 foot of cabinet wood. The profifit of the three types of couches is $10, $8, and $5, respectively. The factory produces 500 couches each month of the fifirst type, 300 of the second type, and 200 of the third type. However, this month there is a shortage of cabinet wood and the supply to the factory will have to be reduced by 600 feet, but the supply of framing wood is increased by 100 feet. How should the production of the three types of couches be adjusted to minimize the decrease in profifit? Formulate this problem as a linear programming problem.
2 Dual Program (15 points) CS 570作业代写
Consider the following linear program:
max(3x1 + 2x2 + x3)
subject to
x1 − x2 + x3 ≤ 4
2x1 + x2 + 3x3 ≤ 6
−x1 + 2x3 = 3
x1 + x2 + x3 ≤ 8
x1, x2, x3 ≥ 0
Write the dual problem.
3 Spectrum Management (10 points) CS 570作业代写
Spectrum management is the process of regulating the use of radio frequencies to promote effiffifficient use and gain a net social benefifit. Given a set of broadcast emitting stations s1, . . . , sn, a list of frequencies f1, . . . , fm, where m ≥ n, and the set of adjacent stations E = {(si , sj )}. The goal is to assign a frequency to each station so that adjacent stations use difffferent frequencies and the number of used frequencies is minimized. Formulate this problem as an integer linear programming problem.
4 Short Questions (15 points) CS 570作业代写
True or false? Shortly explain your answers.
1.If A ≤p B and B is in NP-hard, then A is in NP-hard.
2.If A ≤p B and B is in NP, then A is in NP.
3.If 3 − SAT ≤ p 2 − SAT, then P = NP.
4.Any NP problem can be solved in time O(2poly(n) ), where n is the input size and poly(n) is a polynomial.
5.If a problem A ≤p B, then it follows that B ≤p A.
5 Finding a Satisfying Assignment (10 points) CS 570作业代写
Assume that you are given a polynomial time algorithm that given a 3-SAT instance decides in polynomial time if it has a satisfying assignment. Describe a polynomial time algorithm that fifinds a satisfying assignment (if it exists) to a given 3-SAT instance.
6 Shipping Goods (15 points)
Given n positive integers x1, . . . , xn. The Partition Problem asks if there is a subset S ⊆ [n] such that:
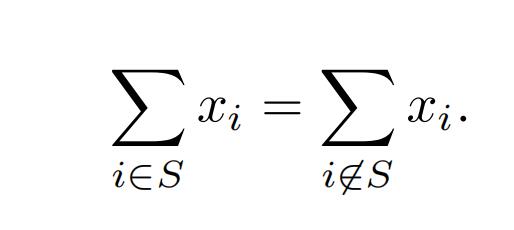
It can be proven that the Partition Problem is NP-complete. You do not to prove it, but rather use it in the following problem. Assume that you are consulting for a shipping company that ships a large amount of packages overseas. The company wants to pack n products with integer weights p1, . . . , pn into a few boxes as possible to save on shipping costs. However, they cannot put any number of products into a box due to the ship-ping capacity restriction. The total weight of products in each box should not exceed W? You may assume that for each i-th product pi ≤ W. You task is to advise the company if n products can be placed into at most k < n boxes. Show that the problem is NP-Complete by reduction from the Partition Problem.
7 Longest Path (15 points) CS 570作业代写
Given a graph G = (V, E) and a positive integer k, the longest-path problem is the problem of determining whether a simple path (no repeated vertices) of length k exists in a graph. Show that this problem is NP-complete by reduction from the Hamiltonian path.
8 Helping with the COVID-19 Crisis (10 points)
Given an integer k, a set C of n cities c1, . . . , cn, and the distances between these cities dij = d(ci , cj ), for 1 ≤ i < j ≤ n, where d is the standard Euclidean distance. We want to select a set H of k cities for building mobile hospitals in light of the coronavirus outbreak. The distance between a given city c and the set H is given by d(c, H) = minh∈H d(c, h). The goal is to select a set H of k cities that minimizes r = maxc∈C d(c, H). Namely, the maximum distance from a city to the nearest mobile hospital is minimized. Give a 2-approximation algorithm for this problem.

其他代写:cs作业代写 homework代写 essay代写 英国代写 web代写 考试助攻 program代写 加拿大代写 北美代写 北美作业代写 数据分析代写 澳大利亚代写 finance代写 Exercise代写
