CS 237—Final Exam
Spring 2020
Cs网课代考 Suppose you select 3 balls from the sack, without replacement, as a What is the probability that the first and third balls are different colors?
You must complete 6 of the 8 problems on this exam for full credit. Each problem is of equal weight. Please leave blank, or draw an X through, or write “Do Not Grade,” on the problem you are eliminating; I will grade the first 6 I get to if I can not figure out your intention—no exceptions! Emphasize your final answers. You may use Wolfram Alpha or a calculator for your calculations.
In writing your answers, remember that your goal is to show me you understand the techniques presented in the course; if you can not completely solve the problem, show me as much as you know and I will attempt to give you partial credit.
Problem One (Poker Probability) Cs网课代考
Suppose you deal a standard five-card poker hand from a well-shuffled deck, without replacement.
(A)What is the probability that you get “three of a kind,” with 3 cards of the same rank (for example, 3 Jacks), and the remaining two cards have the same suit (for example, 2 Clubs). (Note that the 2 remaining cards can not be the same rank as the 3 of a kind, because then it would be 4 of a kind.)
(B)If you turn over two of the cards, and you see that they are the same rank (for example, two Kings), what is the probability that when you turn over the other 3 cards you have “four of a kind” (4 of the same rank) among all fivecards?
Problem Two (Continuous Probability)
Suppose X has a Probability Distribution Function f(x) given by the following graph (the y-axis has been left unspecified on purpose, but you can figure it out easily).
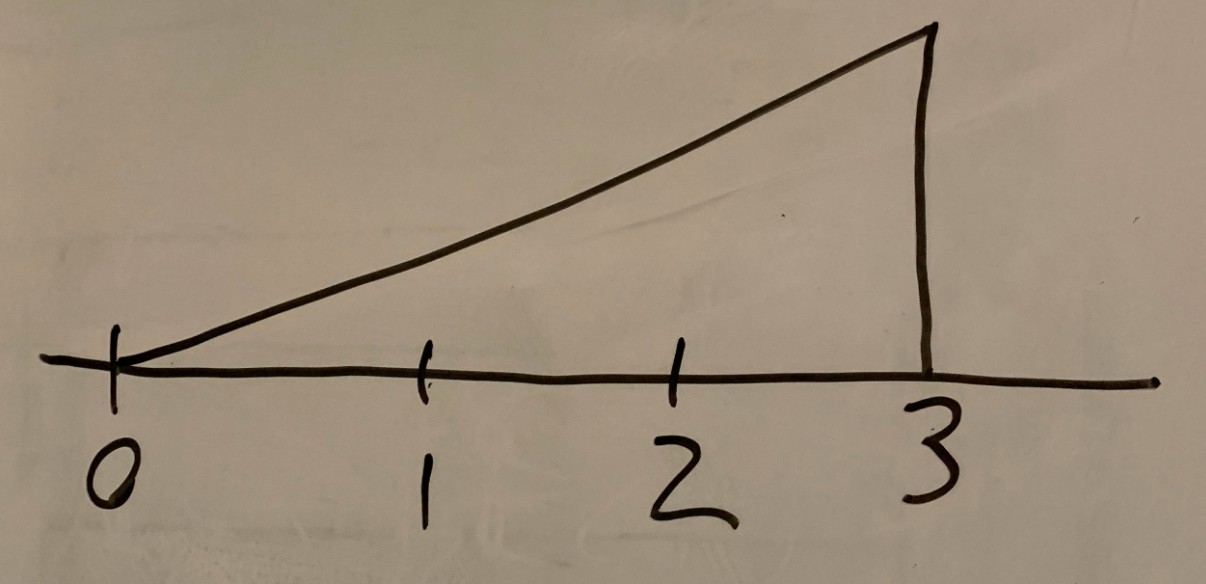
(A)State the PDF f(x) as a mathematical formula.
(B)Calculate the Cumulative Distribution Function F(x) using integrals.
(C)Calculate E(X) using integrals.
Problem Three (Permutations) Cs网课代考
There are 3 red balls in a sack and 5 black balls. Consider each of these situations, which are independent (you start each case with a sack of the 8 red and black balls).
(A)Suppose you select 3 balls from the sack, with replacement, as a What is the probability that the first and third balls are different colors?
(B)Suppose you select 3 balls from the sack, without replacement, as a What is the probability that the first and third balls are different colors?
(C)Suppose you select 3 balls from the sack without replacement and observe that there is 1 red and 2 black. You did not notice which colors came out in which order (they are now just a set of 3 balls). What is the probability that the first ball you selected wasred?

Problem Four (Circular Permutations).
Suppose A, B, C, D, E, F, G, and H are 8 people who must sit together at a round table. Any way of arranging people in seats is the same if it consists merely of rotating people (and empty seats) around the tables (e.g., everyone moves 2 seats clockwise).
Show all work! You may leave (correct) formula uncomputed if you wish. Each of these questions is independent and represent separate problems.
(A)Suppose A and B must sit together (no person can sit between them) and C and D can NOT sit together. How many ways of arranging this group arethere? Cs网课代考
(B)Suppose A, B, C, and D are women and the rest are men. Supposing all the women must sit together (no man can sit between two women), how many ways of arranging this group arethere?
(C)Suppose A and B insist on sitting as far apart as possible (meaning directly across the table, with 3 people between them on each side). How many ways of arranging this group arethere?
Problem Five. (Normal Distribution)
Suppose the expected lifetime of the Barracuda disk drive made by Seagate is a normal random variable with mean 10,000 hours and standard deviation 1000 hours.
[For this problem, use the normal table posted on the class web site, or Google “Normal Distribution Calculator” or use a Jupyter notebook with the appropriate library functions for the normal distribution].(A)Is this company correct when it claims that at least 90% of its Barracuda drives lastat least 8500 hours?
(B)Supposing a testing company tests by taking 25 of the disk drives and running them until failure, and then taking the mean of the lifetimes. What would be the expected mean and standard deviation of the resulting sampling distribution ofmeans?
(C)Supposing we wanted to get more accuracy in our sampling procedure in part (B),so that we wanted the standard deviation of the sampling distribution of means to be at most 150 hours. What is the smallest sample size we could use to insure this?
Problem Six (Poisson and Exponential) Cs网课代考
Suppose the probability that the T arrives at BU Central is modelled as a Poisson random variable with rate parameter λ = 3 arrivals per hour.
(A)This exam lasts 4 hours; what is the probability that exactly 10 arrivals occur during the exam? (Give the formula.)
(B)Suppose after the exam you arrive at the T stop at precisely 4pm and wait for half an hour and no T shows up. What is the probability that one will show up in the next half an hour? (Use Poisson.)
(C)The interarrival times for the T can be modelled using the Exponential What precisely is the exponential distribution involved in parts A and B (give the parameter)? What is the probability that if you just miss the T, you will have to wait at least 20 minutes for the next one? (Use Exponential.)
(D)As you wait at the T, you hear one of your classmates saying that he aced Part B of question Six because he remembered that the Poisson Distribution and the Exponential are very similar, and the Poisson has the Memory-less Property. However, checking your notecard, you see that only the Geometric and Exponential distributions have this property. How would you correct your friend’s misunderstanding? What property does the Poisson distribution have that helped you answer (B) and that might have caused the confusion?
Problem Seven (Lab Problem: Regression)
The following problems are all based on the linear regression of the following data, diagram shown at the right.
{ (0,1), (2,0), (1,1), (1,0) } or X = { x0, x1, x2, x3 } = { 0, 2, 1, 1 }
Y = { y0, y1, y2, y3 } = { 1, 0, 1, 0 }
(A)Give the predicted list ofvalues:
![]()
= { }
Give the list of residuals or errors:
E = { e0, e1, e2, e3 }
= { }
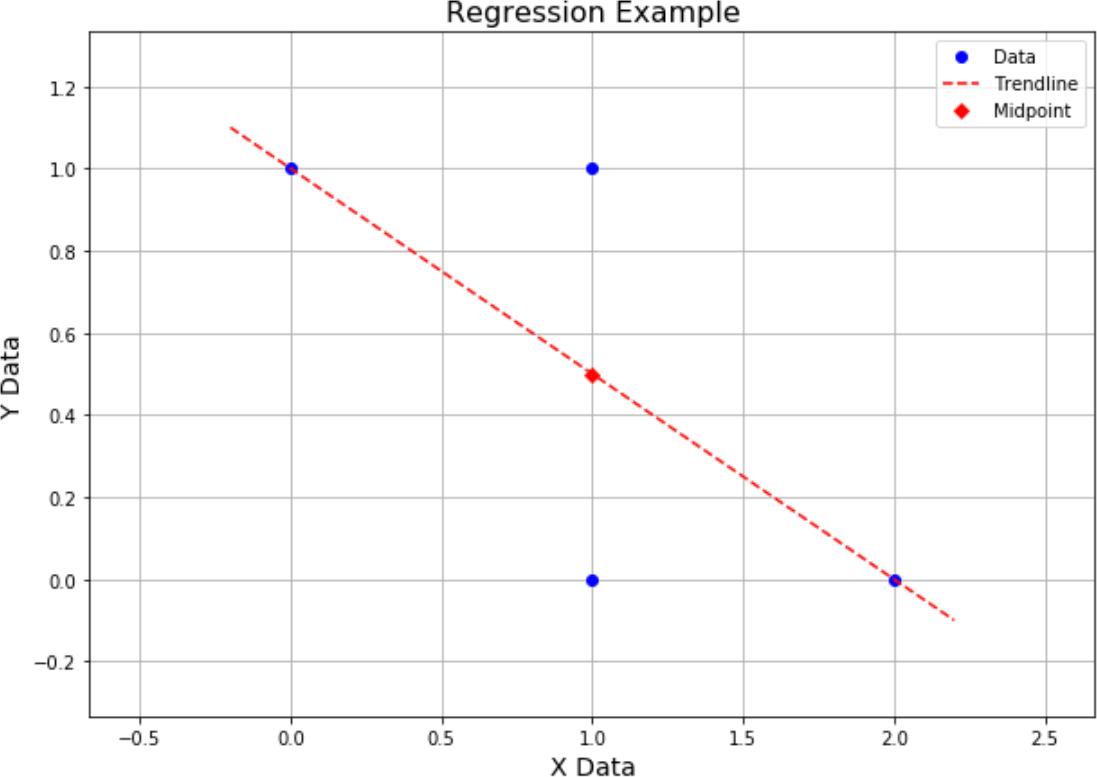
(C)Calculate the correlation coefficient ρ of this data (either by hand or using code from a notebook, say for homework 10) and show precisely how the equation for the line is calculated.
(D)Suppose after you do all this calculation and drawing, you find out that the Y values actually encode experimental results “1 = success” and “0 = failure” (so there are no values other than 0 and 1 possible on the Y axis). What does the regression line mean in this case? Would there be a more appropriate way to analyze this data (answer this last question in a brief sentence, not anessay)?
Problem Eight (Lab Problem – Queueing Simulation)
In HW 9 we studied a quite realistic queueing simulation using the Exponential Distribution. In this problem, you will reflect on what you learned in that experience.
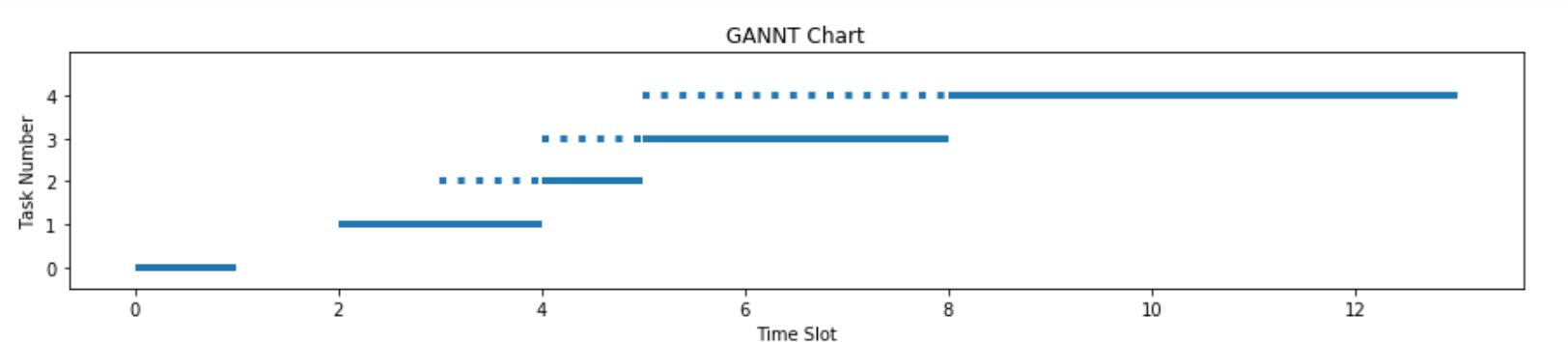
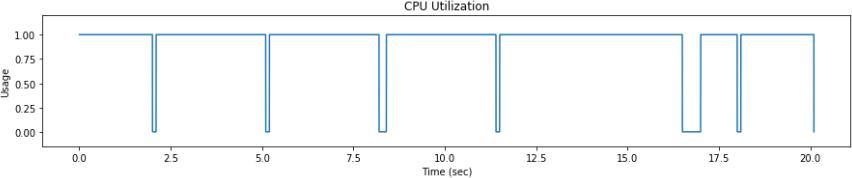
(A)What is the CPU utilization of the system described by the GAANT chart to theright?
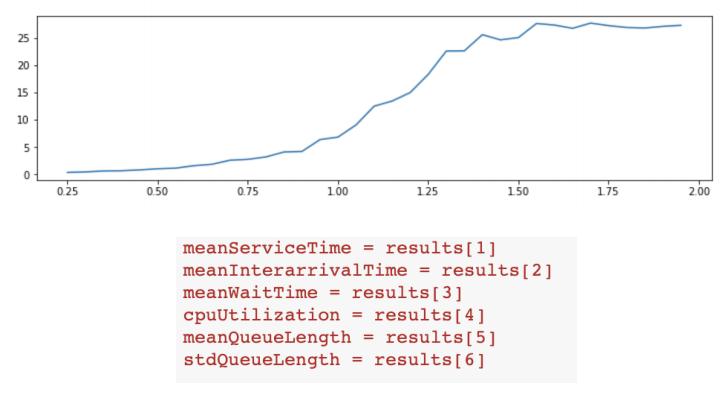
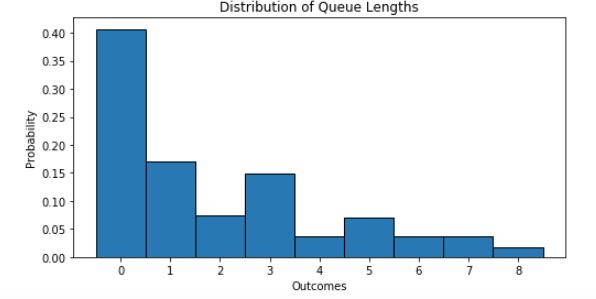
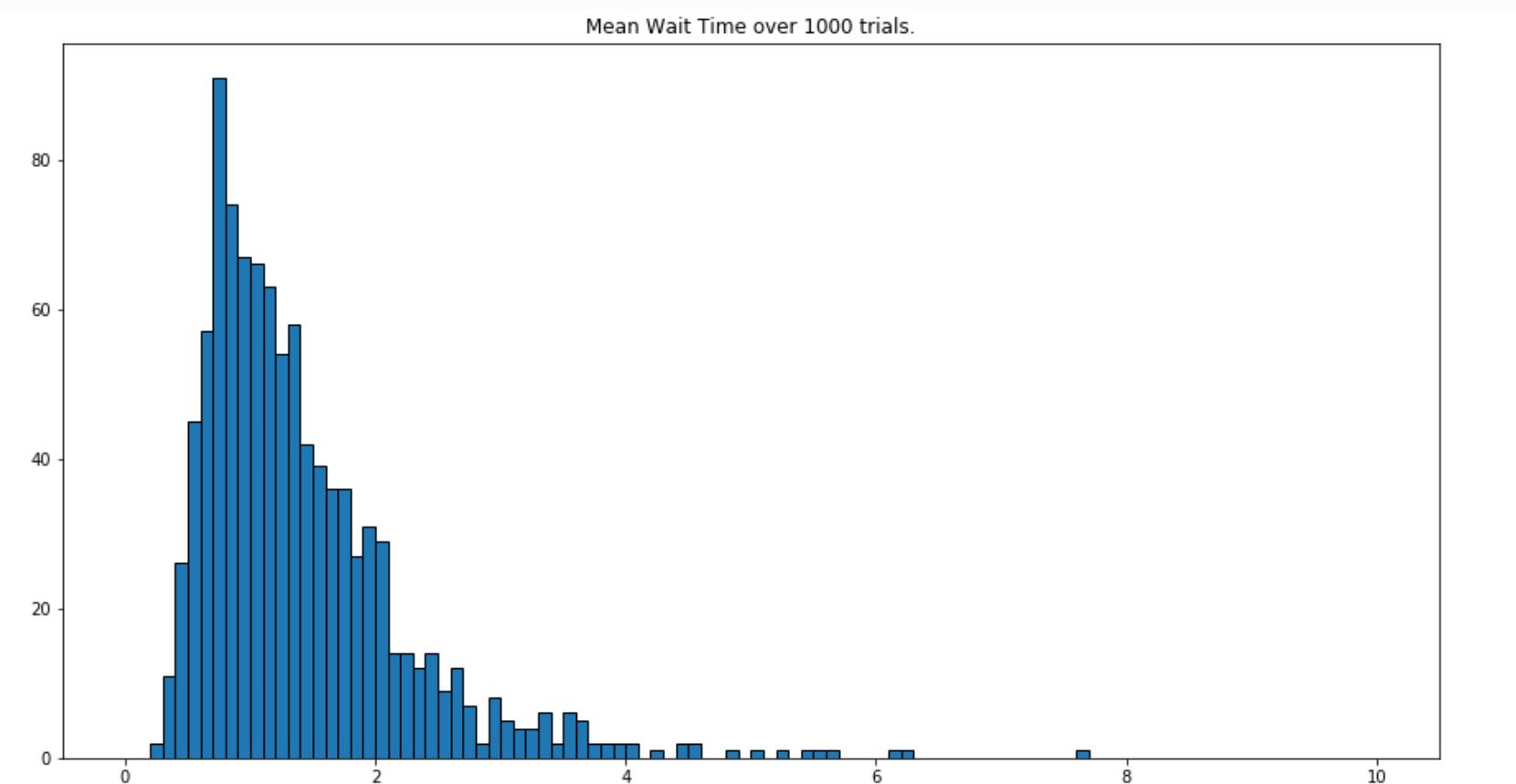
(B)Consider the familiar graph to the right and the list of parameters we Which parameters could this possibly be a graph for? (Youmay just give the number if you wish, e.g. “6” for “stdQueueLength.”)
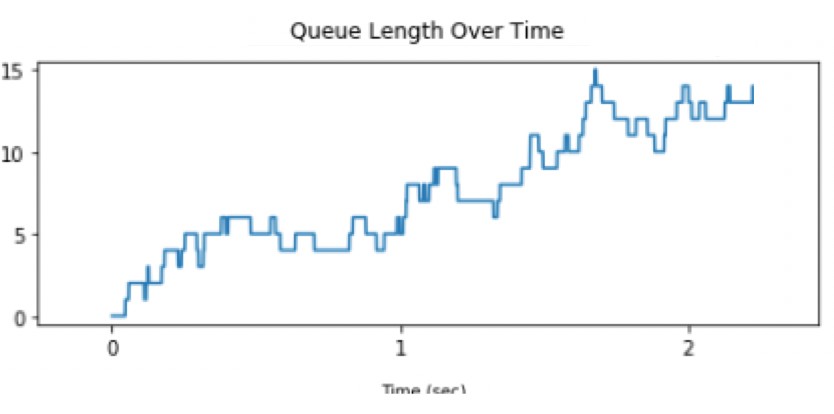
(C)Consider the following diagrams similar to those in HW9.
Do they indicate a system in overload? Label each of them as “NO”, “YES,” or “Maybe.”

更多代写:Online exam代考价格 多邻国代考 管理类assignment代写 Persuasive Speech代写 管理论文代写 代写SPSS分析价格
