CS181 Winter 2019 – Final
CS期末代考 his exam is open-book and open-notes, but any materials not used in this course are prohibited, including any material found
Name:
Student ID:
Due Friday, March 15, 11:59 PM
-
This exam is open-book and open-notes, CS期末代考
but any materials not used in this course are prohibited, including any material found on the internet. Collaboration is prohibited. Please avoid temptation bynot working on the final while you are in the presence of any other student who has taken or is
currently taking CS181. Be extra careful if you live with or meet regularly with a student of this class. If you have any questions about the exam, ask the TA or Professor Sahai by email or after class. Do not ask other students. You are allowed to use any theorem shown in class or in the textbook, as long as you clearly cite it. Please monitor Piazza for any clarifications. Do not post any questions on piazza.CS期末代考
- We suggest that you spend approximately 12 hours (not necessarily contiguous) to take this exam. Start early so that you have time to understand and think about the problems. The solutions mustbe
submitted on Gradescope by 11:59 PM on Friday, March 15.CS期末代考
- Place your name and UID on every page of your solutions. Retain this cover sheet and the next sheet withthe table as the first pages of your Please use separate pages for each question.CS期末代考
All problems require clear and well-written explanations.
- Thereare 4 questions worth a total of 230 points and an extra credit question worth 40
- For each part (except for the extra credit), if you describe a non-trivial approach that you tried using to solvethe problem but realized it doesn’t work and explain correctly why it doesn’t work and then write “I don’t know” you will get 20% points for that problem. You will not get 20% points for just writing “I don’t know”. Whether your stated approach was indeed non-trivial is solely at the discretion of the grader.CS期末代考
- 5%extracredit will be awarded to solutions written in LATE

1. Decidability/Recognizability (60 points)
Height
For a Turing machine M , let height(M ) denote the length of the shortest string accepted by M (or ∞ if
M does not accept any string). Consider the following language
Lheight = {(M ) | height(M ) < |(M )|},
that is the language of Turing machines that accept a string that is shorter than their own description.
a)(15 points) Show that Lheightis
b)(15 points) Show that Lheightis CS期末代考
For all parts, remember to first write your intuition before writing your formal solution.

Trump MachineCS期末代考
A Turing machine M over alphabet Σ = {0, 1, $} and tape alphabet Γ = {H, 0, 1, $, #} is a Trump machine if for all x ∈ Σ∗ such that x contains at least 5.7 billion $ symbols, during the execution of M on input x, M erases all $ symbols from its tape (replaces them with blanks), writes a single wall symbol #, and
then shuts down (either accepts or rejects). Let
LTrump = {(M ) | M is a Trump machine}.
c)(15 points) Show that LTrumpis
d)(15 points) Show that LTrumpis
For all parts, remember to first write your intuition before writing your formal solution.期末考试代写
2. Inconclusive Decider (40 points)
An Inconclusive Decider is like a decider except that on some set of inputs, instead of accepting or reject- ing, it may instead halt and output “INCONCLUSIVE”.
Formally, we say that a language L is k-Inconclusive-Decidable for some k ∈ N ∪ {∞} if there exists a Turing machine M such that
- For all x such that x ∈ L, M either halts and outputs “ACCEPT” or halts and outputs “INCONCLUSIVE”.
- Forall x such that x ∈/ L, M either halts and outputs “REJECT” or halts and outputs “INCONCLUSIVE”.
- Mhalts and outputs “INCONCLUSIVE” on at most k distinct inputs x.CS期末代考
(Note that L is decidable if and only if it is 0-Inconclusive-Decidable)
a)(5 points) Show that all languages are∞-Inconclusive-Decidable.
b)(20 points) Show that LHaltε = {(M ) | M (ε) halts} is not1-Inconclusive-Decidable.
c)(15 points) Show that LHaltε = {(M ) | M (ε) halts} is not2-Inconclusive-Decidable.
For all parts, remember to first write your intuition before writing your formal solution.CS期末代考
3. Perpetual Machines (70 points)
An perpetual machine P is like a Turing machine, except that it never halts on any input. Instead of containing accept and reject states, qaccept and qreject, it contains a non-halting accepting state q∗. When P enters q∗, instead of terminating its computation, it continues executing and can transition out of this state.
A perpetual machine P computes a language L if
- For all x ∈ L, P (x) enters q∗an infinite number of times
- For all x ƒ∈L, P (x) does not enter q∗ an infinite number of times
If there does not exist any perpetual machine P that computes a language L, we say that L is uncom- putable by perpetual machines.CS期末代考
a)(25 points) Show that thelanguage
Lloop = {(M ) | M is a Turing machine and M (ε) loops} is computable by perpetual machines.
b)(20 points) Construct a language L ⊆ Σ∗that is uncomputable by perpetual machines and prove that this is the case. (Hint: Use diagonalization)
c)(25 points) Show that thelanguage
LEmpty = {(M ) | M is a Turing machine and L(M ) = ∅}
is computable by perpetual machines.Final Exam2代写
d)(Extra Credit, 40points) Show that the language
LEQ = {((M1), (M2)) | M1 and M2 are Turing machines and L(M1) = L(M2)}
is computable by perpetual machines.
For all parts, remember to first write your intuition before writing your formal solution.
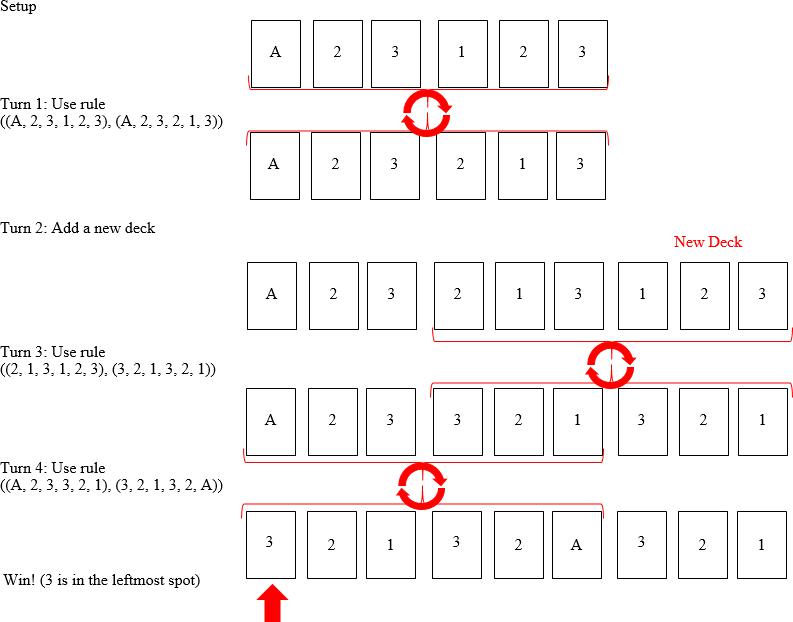
4. Card Shuffling (60 points)CS期末代考
Let C = (N, R) be a card-shuffling game, described by a natural number N and a set of allowed card- shuffling rules R. We introduce some notation and define the game below.CS期末代考
- Normal Deck: A deck of N cards labeled (1, 2, 3, …, N).
- Ace Deck: A normal deck but with the first card replaced by an Ace. In other words, a deck ofN
cards labeled (A, 2, 3, …, N ).
- Shuffling Rule: A shuffling rule specifies an allowed shuffle (permutation) of any finite number of cards.In particular, each rule is a tuple ({A, 1, 2, …, N }k, {A, 1, 2, …, N }k), where the left side of thetuple specifies the card sequence that can be shuffled with this rule, and the right side of the tuplespecifies the new card sequence after the shuffle. For example, ((2, 7, 4, 1), (1, 2, 4, 7)) means that ifwe see cards labeled 2, 7, 4, 1 next to each other in this order, then we can shuffle/rearrange them tobe in the new order of 1, 2, 4, 7. R is the set of allowed shuffling rules and is a subset of the set of allpossible shuffles.CS期末代考
- Game Setup: In a row, we place face-up the cards of an Ace deck in order and then place face-up the cards of a normal deck in

-
Gameplay: Each turn, we may do one of thefollowing:
- Add a normal deck: Place face-up the cards of a normal deck in order to the right of all cards currently
- Perform a shuffle: Choose any number of consecutive cards and shuffle them according to some allowed shuffle rule in R. In other words, choose any number of consecutive cards that are in the order specified in the left hand side of some rule in R, and then reorder them to be in the orderspecified by the right hand side of the same
- Win Condition: You win if you can get a card labeled N into the leftmost card position by playing this game. You can use as many turns as you (See example on nextpage.)
Let L = {C = (N, R) | It is possible to win game C}. Prove that L is undecidable.
Hint: Consider shuffles of 2N or 3N cards. CS期末代考
You may assume that every TM can be converted into an equivalent TM that will never try to move left on the leftmost tape position, and if this new TM halts, it always halts when the head is at the leftmost tape position.
Remember to first write your intuition before writing your formal solution.
Example:
Let C = {3, {((A, 2, 3, 1, 2, 3), (A, 2, 3, 2, 1, 3)), ((2, 1, 3, 1, 2, 3), (3, 2, 1, 3, 2, 1)), ((A, 2, 3, 3, 2, 1), (3, 2, 1, 3, 2, A))}.Then, you can win game C after four turns.

更多其他:考试助攻 C语言代写 finance代写 计算机代写 report代写 project代写 物理代写 数学代写 经济代写 java代写 python代写 程序代写 金融经济统计代写
