残差散点图 偶遇一份关于树木根基属性的数据,某研究者想探讨体积(y)和树高(x1)、周长(x2)的相关干系,因变量体积y是定量变量,所以我们推荐线性回归举办阐明。为了验证模子是否满意线性回归的前提条件,我们可以通过残差散点图举办判定。详细的判定要领可查察本公家号往期文章《多重线性回归前提条件的应对》,下图是拟合线性回归方程y~x1+x2,所获得残差散点图,纵坐标是残差,横坐标是预测值。
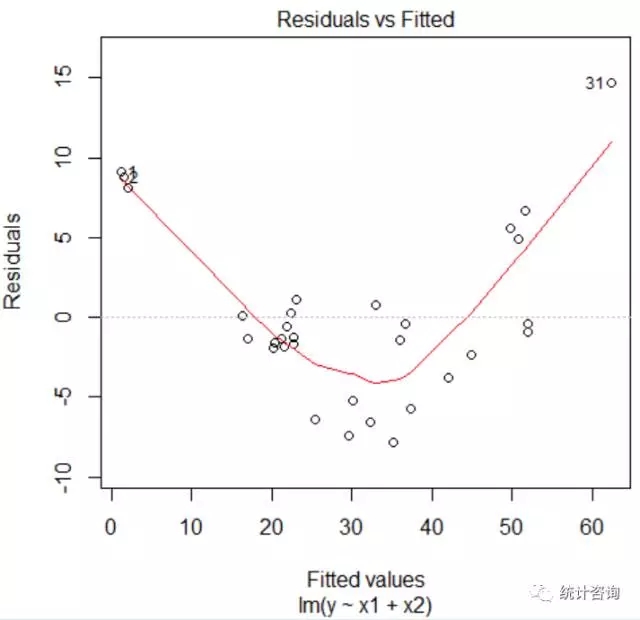
非线性漫衍 从上图可知,我们所拟合的回归方程存在明明的非线性干系。虽然,我们可以通过直接拟合广义线性模子或非线性模子等,来处理惩罚非线性的问题,但这凡是是最后的杀手锏,明智的做法应该是先回收相对简朴的数据调动要领来实验处理惩罚该类问题。数据调动可以对自变量举办,也可以对因变量举办,但往往思量到拟合方程后对功效的可表明性,我们凡是选择对自变量举办调动,合用于自变量做正态调动的要领可以查察本公家号往期文章《数据不正态,怎么办?》。
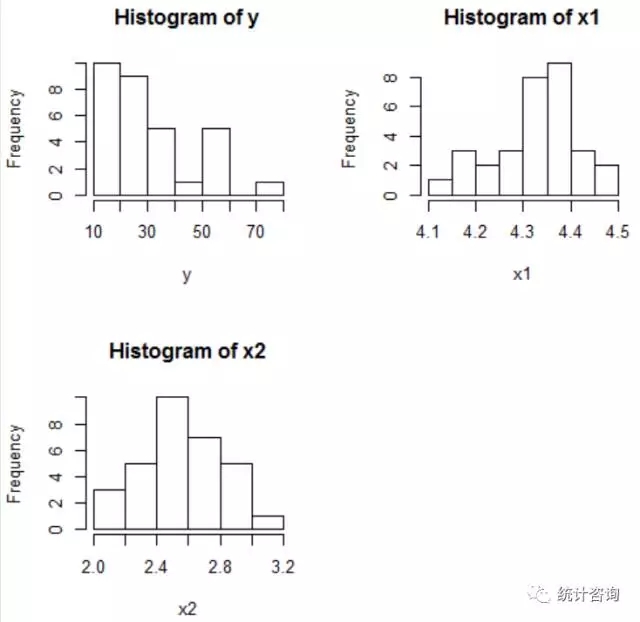
我们先通过直方图(见下图)考查一下各个变量的漫衍环境,发明自变量都根基切合正态漫衍的环境,存在问题的正是因变量,它呈明明的正偏峰漫衍。所以接下来我们思量如何对因变量举办调动。
Box-Cox调动公式
除了上面碰着的例子,出格是在医学统计阐明中,常会碰着因变量不满意正态漫衍的环境,我们就可以对因变量举办调动,Box-Cox调动是最常用的一种要领。Box-Cox调动的道理很简朴,用两个公式就可以很好地表明。第一个公式为:
y’=(y+c)^λ-1/[λ*g^(λ-1)]y’是调动后的因变量;g为因变量y的几许均数;当因变量y存在小于便是0的数据时,我们需要借助参数c对整个因变量数据举办平移,使得y+c>0;λ为最重要的调动参数,可以通过极大似然法举办预计,当所预计的λ为0时,上面的公式恒便是0,所以需要校正为以下公式:
y’=g*log(y+c)
R语言实例 下面我们回收R语言对开篇的例子举办Box-Cox调动以及调动后的回归阐明。
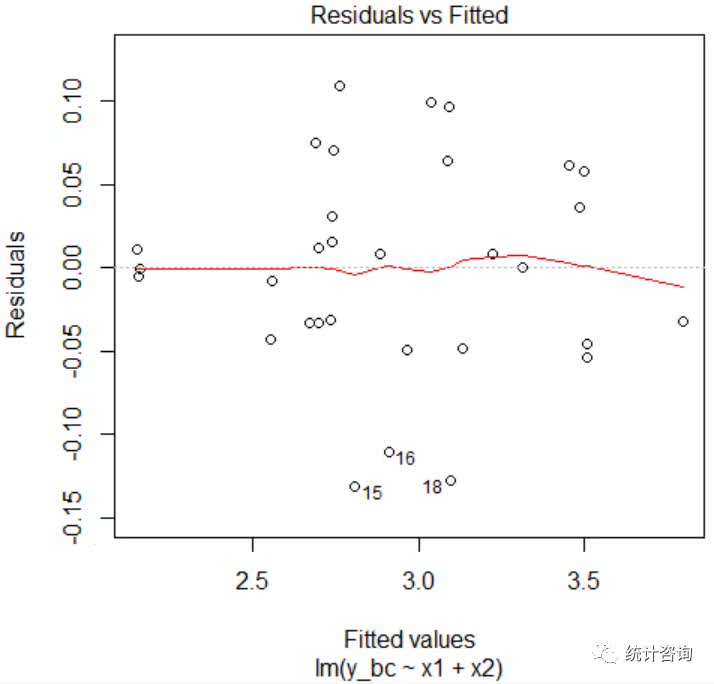
#载入car包library(car)#预计调动参数λlambada=powerTransform(y~x1+x2)#举办Box-Cox调动y_bc=bcPower(y,lambda$lambda)#调动后的线性回归fit=lm(y_bc~x1+x2)#查察残差散点图plot(fit)
由散点图可知,通过Box-Cox调动后,残差散点的漫衍环境获得明明的改进,根基切合前提假设。
参考文献 Box, G. E. P. and Cox, D. R. (1964). An analysis of transformations, Journal of the Royal Statistical Society, Series B, 26, 211-252.Kutner, M., Nachtsheim, C., Neter, J., and Li, W. (2004). Applied Linear Statistical Models, McGraw-Hill/Irwin, Homewood, IL.
接待插手本站果真乐趣群贸易智能与数据阐明群乐趣范畴包罗各类让数据发生代价的步伐,实际应用案例分享与接头,阐明东西,ETL东西,数据客栈,数据挖掘东西,报表系统等全方位常识QQ群:81035754
