Intro to AI HW3
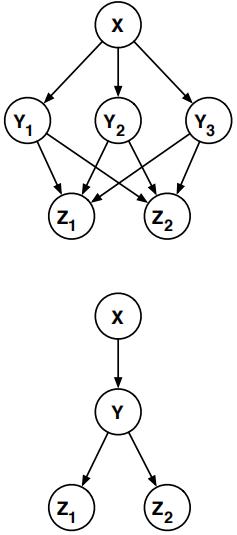
Artificial Intelligence作业代写 The network can be transformed into a polytree by clustering the nodes Y1, Y2, and Y3 into a single node Y .
3.1 Variable Elimination Algorithm
Consider the following belief network with binary random variables.
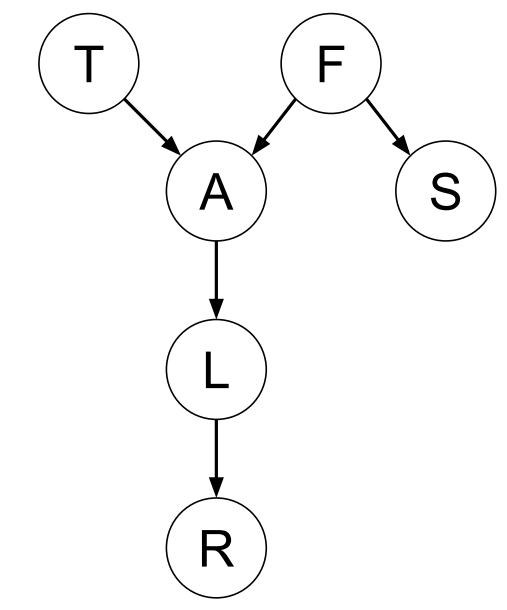
(Source: Adapted from Poole and Mackworth, Artificial Intelligence 2E, Section 8.3.2. For a description of the meaning of the variables in this belief network, see Example 8.15.)
Suppose we want to compute a probability distribution over T given the evidence S = 1 and R = 1. That is, we want to compute P (T = 0 S = 1, R = 1) and P (T = 1 S = 1, R = 1). In this question, we will evaluate the efficiency of two different methods of computing these probabilities.
The conditional probabilities of this belief network (expressed as factor tables) are as follows:
Note that the conditional probabilities are specified with some redundancy. For example, the tables store both P (A = 0|T = 1, F = 1) and P (A = 1|T = 1, F = 1), even though this information is technically re- dundant. Therefore, no addition or subtraction operations are required to compute P (A = 0|T = 1, F = 1) based on P (A = 1|T = 1, F = 1) or vice versa.
(a) Computation using variable elimination
Use the variable elimination algorithm (with elimination order S, R, L, A, F ) to compute
P (T = 0|S = 1, R = 1) and P (T = 1|S = 1, R = 1).
You do not need to write code for this; you should apply the algorithm step-by-step and show your work, including any new factor tables that are computed along the way.
(b) Counting calculations used by the variable elimination algorithm
In the following table, fill in the number of multiplication, addition, and division operations neededfor each phase of the VE algorithm. You should count operations using the same method used in class: for example, a × b + c × d + e × f involves 3 multiplications and 2 additions.
| Phase of algorithm | # multiplications | # additions | # divisions |
| Eliminate S (evidence) | 0 | 0 | 0 |
| Eliminate R (evidence) | 0 | 0 | 0 |
| Eliminate L | 0 | ||
| Eliminate A | Artificial Intelligence作业代写 | 0 | |
| Eliminate F | 0 | ||
| Combine T factors | 0 | ||
| Normalize distribution over T | 0 | 1 | 2 |
| Total | 2 |
(c) Counting calculations used by the enumeration algorithm
In the brute-force enumeration method, we can compute the desired probabilities via
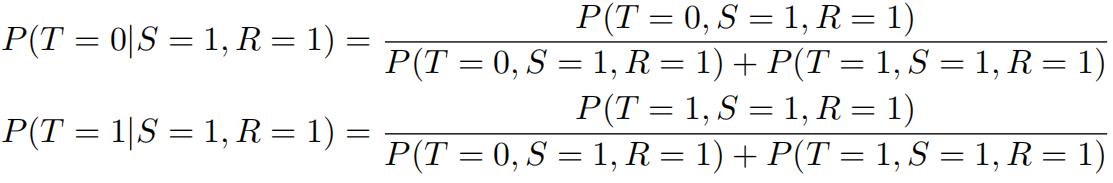
That is, we compute P (T = 0, S = 1, R = 1) and P (T = 1, S = 1, R = 1) and then normalize to obtain a probability distribution over T .
In the following table, fill in the number of multiplication, addition, and division operations needed for each phase of this algorithm. Assume that the algorithm does a full brute-force calculation, even if some operations are redundant.
| Phase of algorithm | # multiplications | # additions | # divisions |
| Compute P (T = 0, S = 1, R = 1) | 0 | ||
| Compute P (T = 1, S = 1, R = 1) | 0 | ||
| Normalize distribution over T | 0 | 1 | 2 |
| Total | 2 |

3.2 To be, or not to be, a polytree: that is the question. Artificial Intelligence作业代写
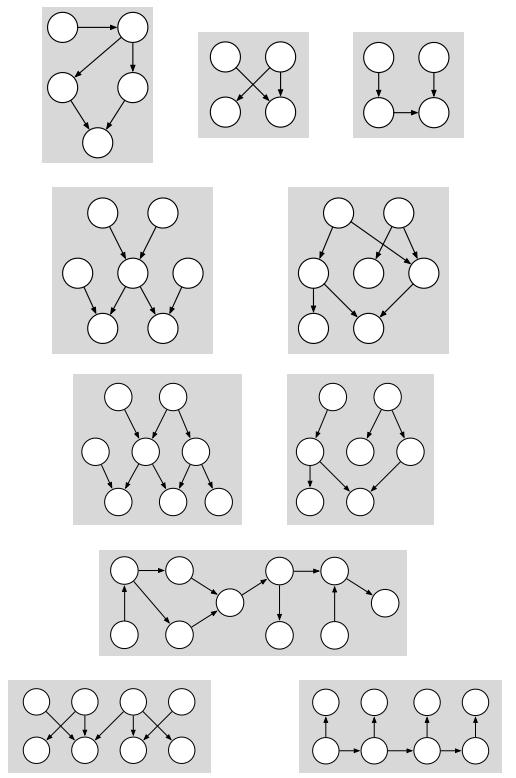
Circle the DAGs shown below that are polytrees. In the other DAGs, shade two nodes that could be clustered so that the resulting DAG is a polytree.
3.3 Node clustering Artificial Intelligence作业代写
Consider the belief network shown below over binary variables X, Y1, Y2, Y3, Z1, and Z2. The network can be transformed into a polytree by clustering the nodes Y1, Y2, and Y3 into a single node Y . From the CPTs in the original belief network, fill in the missing elements of the CPTs for the polytree.
| X | P (Y1 = 1|X) | P (Y2 = 1|X) | P (Y3 = 1|X) |
| 0 | 0.85 | 0.30 | 0.50 |
| 1 | 0.25 | 0.35 | 0.70 |
| Y1 | Y2 | Y3 | P (Z1 = 1|Y1, Y2, Y3) | P (Z2 = 1|Y1, Y2, Y3) |
| 0 | 0 | 0 | 0.8 | 0.2 |
| 1 | 0 | 0 | 0.7 Artificial Intelligence作业代写 | 0.3 |
| 0 | 1 | 0 | 0.6 | 0.4 |
| 0 | 0 | 1 | 0.5 | 0.5 |
| 1 | 1 | 0 | 0.4 | 0.6 |
| 1 | 0 | 1 | 0.3 | 0.7 |
| 0 | 1 | 1 | 0.2 | 0.8 |
| 1 | 1 | 1 | 0.1 | 0.9 |
3.4 Maximum likelihood estimation for an n-sided die Artificial Intelligence作业代写
A n-sided die is tossed T times, and the results recorded as data. Assume that the tosses x(1), x(2), . . . , x(T ) are identically distributed (i.i.d.) according to the probabilities pk = P (X = k) of the die, and suppose that over the course of T tosses, the kth side of the die is observed Ck times.
(a) Log-likelihood
Express the log-likelihood = log P (data) of the observed results x(1), x(2), . . . , x(T ) in terms of the probabilities pk and the counts Ck. In particular, show that
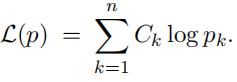
(b) KL distance
Define the distribution qk = Ck/T , where T = ![]() Ck is the total number of counts. Show that
Ck is the total number of counts. Show that
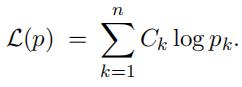
where KL(q, p) is the KL distance from homework problem 1.6. Conclude that maximizing the log- likelihood in terms of the probabilities pk is equivalent to minimizing the KL distance KL(q, p) in terms of these same probabilities. (Why is this true?)
(c) Maximum likelihood estimation
Recall from homework problem 1.6b that KL(q, p) 0 with equality if and only if qk = pk for all k. Use this to argue that pk = Ck/T is the maximum-likelihood estimate—i.e., the distribution that maximizes the log-likelihood of the observed data. Artificial Intelligence作业代写
Note: you have done something quite clever and elegant here, perhaps without realizing it! Generally speaking, to maximize the log-likelihood in part (a), you need to solve the following optimization:

This is a problem in multivariable calculus requiring the use of Lagrange multipliers to enforce the constraint. You have avoided this calculation by a clever use of the result in homework problem 1.6.

更多代写:生物学Biology网课代修 GMAT代考 会计网课代上推荐 美国留学商科essay代写 美国会计论文代写 case study是什么

