STATGU4206_GR5206_Midterm
Gabriel Young 10/18/2018
The STAT GU4206/GR5206 Fall 2018 Midterm is open notes, open book(s), open computer and online resources are allowed. Students are not allowed to communicate with any other people regarding the exam with the exception of the instructor (Gabriel Young) and course TAs. This includes emailing fellow students, using WeChat and other similar forms of communication. If there is any suspicion of one or more students cheating, further investigation will take place. If students do not follow the guidelines, they will receive a zero on the exam and potentially face more severe consequences. The exam will be posted on Canvas at 8:35AM. Students are required to submit both the .pdf and .Rmd files on Canvas (or .html if you must) by 11:30AM. If students fail to knit the pdf or html file, the TA will take off a significant portion of the grade. Students will also be significantly penalized for late exams. If for some reason you are unable to upload the completed exam on Canvas by 11:30AM, then immediately email markdown file to the course TA.
Note: If you have a bug in your code then RMarkdown will not knit. I highly recommend that you comment out any non-working code. That way your file will knit and you will not be penalized for only uploading the Rmd file.
For online students: Online students are required to be logged into the Zoom meeting with their cameras on. The TA will be available to answer questions during the Zoom exam. The Exam shouldn’t take the whole period so I expect for students to have their knitted file uploaded by 11:30AM.
For in-class students: In-class students are required to be physically present in Room 903. The TA/instructor will be available to answer questions during the exam. The Exam shouldn’t take the whole period so I expect for students to have their knitted file uploaded by 11:30AM.
Section 1 – Bootstrap and Robust Estimation
Problem Statement:
Consider the following toy dataset relating response variable Y with covariate X. Note that this dataset is an extreme case of how traditional least squares regression fails to capture the trend of the the data in the presences of outlying observations.
data <- read.csv(“Problem1.csv”) plot(data$X,data$Y,main=“Linear Trend and Outlyers”)
Linear Trend and Outlyers
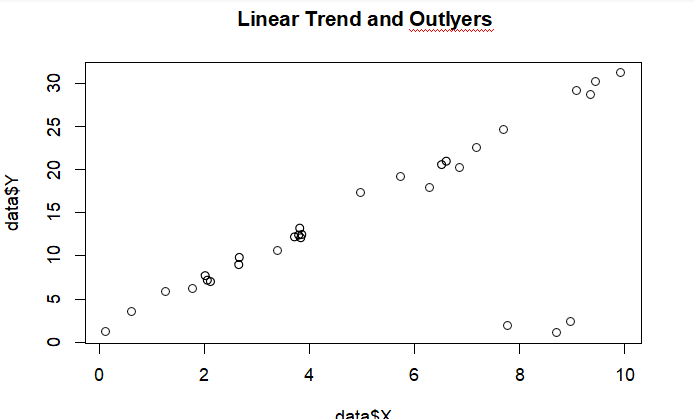
Problem 1:
Fit a regular linear regression to the above dataset and plot the line of best fit in red.
Also remove the three outlying points and fit the linear model on the remaining 27 cases. Plot this new line of best fit on the same graph as the first model. Create a legend on the plot describing each line. Note: remove the points corresponding to Y = 1.05, 1.94, 2.38.
Comment on any interesting features from the graph and estimated models.
Solution
# Solution goes here ————
Problem 2 Set-Up:
To fit the linear model, we minimize the total squared Euclidean distance between Y and a linear function of
X, i.e., minimize the expression below with respect to β0, β1.
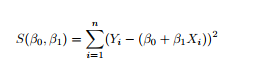
From the above fit, we see that the outlying Y values are influencing the estimated line, consequently, the linear fit is being pulled down and is not covering the full trend of the data. To remedy this problem, we can perform a robust estimation procedure. More specifically, instead of minimizing squared Euclidean distance (squared loss), we can minimize Huber loss. To estimate our robust model, we minimize Q(β0, β1) with respect to β0, β1:
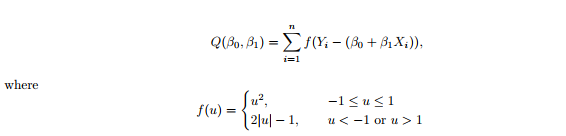
The goal of the next exercise is to write a robust estimation procedure for the coefficients β0, β1. In class we performed univariate gradient descent. On this exam, we will use the R base function nlm() to perform the optimization task. Below shows how the non-linear minimization function is applied to minimize squared Euclidean distance.
# First define an objective function
S <- function(betas,response=data$Y,feature=data$X) { b0 <- betas[1]
b1 <- betas[2]
lin.diff <- response–(b0+b1*feature) out <- sum((lin.diff)^2)
return(out)
}
# Test S(beta0=1,beta1=1)
S(betas=c(0,0))
## [1] 8207.36
# Use starting point c(beta0=1,beta1=1). The estimated
## $minimum
## [1] 1415.941 ##
## $estimate
## [1] 3.769193 1.987186 ##
## $gradient
## [1] 7.552595e-05 4.119117e-06 ##
## $code ## [1] 1 ##
## $iterations ## [1] 3
# Compare estimates to lm()
nlm(S,p=c(0,0))$estimate
## [1] 3.769193 1.987186
lm(Y~X,data=data)$coefficients
## (Intercept) X ## 3.769174 1.987190
Note that in this example, the nlm() function produces very similar estimates as the lm() function.
Problem 2:
Write a R function Q which computes the Huber loss as a function of the vector c(β0, β1). Note that the Huber loss is defined in Equation (1). This exercise is having you create an objective function Q(β0, β1) so that you can run an optimization procedure later on. Test your function at the point c(0,0).
Solution
# Solution goes here ————
Problem 3:
Optimize Huber loss Q using the nlm() function. Use the starting point c(0,0) and display your robust estimates. Plot the estimated robust linear model and include the regular least squares regression line on the plot. Create a legend and label the plot appropriately.
Solution
# Solution goes here ————
Problem 3 Set-Up:
As statisticians, we must also construct confidence intervals on our parameter estimates to gauge how precise these estimates actually are. Recall the traditional parametric regression model:
![]()
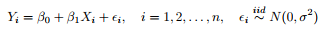
When using least squares estimation, the normal-error structure (si ∼ N (0, σ2)) allows us to construct
iid
parametric confidence intervals for the parameters β0, β1. This is easily done in R. The code below constructs 95% intervals for the coefficients.
round(confint(lm(Y~X,data=data),level=.95),4)
![]()
## 2.5 97.5
## (Intercept) -1.6034 9.1418
## X 1.0711 2.9032
Notice from the above output, the slope is almost not within the range of what we expect. Clearly the outliers are impacting our least squares estimators. In the presence of our outlying observations, the normal error structure is clearly not correct. To approximate the correct distribution, we will apply the bootstrap procedure on the robust estimated coefficients computed by minimizing Q(β0, β1).
Problem 3:
Bun a bootstrap on the robust estimation procedure. Note that this is similar to the regression bootstrap but you will be estimating the parameters by minimizing Q(β0, β1). Use B = 1000 bootstrap iterations
and confidence level 95%. Use the regular bootstrap intervals (not percentile intervals) and compare your bootstrapped solution to the parametric model.
Solution
# Solution goes here ————
Part II Regular Expressions and Textual Data
In this example, we consider the html file ScaryGoodIMDb.html which includes the to the top 35 highest grossing R rated horror films. Open the html file to see the actual webpage and get a feel for the titles on their list.
|
## |
[1] |
“” |
|
## |
[2] |
“” |
|
## |
[3] |
“” |
|
## |
[4] |
“<!DOCTYPE html>” |
|
## |
[5] |
“<html” |
|
## |
[6] |
|
|
## |
[7] |
|
|
## |
[8] |
“ <head>” |
|
## |
[9] |
“ “ |
|
## |
[10] |
“<script type=‘text/javascript‘>var ue_t0=ue_t0||+new Date();</script>” |
Problem 4:
Consider the following regular expression related to the movie Zombieland: href=“/title/tt1156398/”>Zombieland (2009)Domestic Gross: $75,590,286
# Solution goes here ———— # Zombieland_exp <-
# grep(pattern=Zombieland_exp,ScaryGood)
Copy and paste the regular expression below and fix any special characters so that the grep() function recognizes this pattern. Run the grep function and display what line the pattern shows up on.
Problem 5:
Use the functions grep(), gregexpr() and regmatches() to extract the character string pattern from the
ScaryGoodIMDb.html file. Show the pattern below, i.e., run the regmatches() function.
Solution
# Solution goes here ————
Problem 6:
Generalize the working regular expression Zombieland_exp so that it will work with any movie. Again use the functions gre(), gregexpr() and regmatches() to extract the character string pattern from the ScaryGoodIMDb.html file. Note that regmatches() returns a list so you will want to extract the first (and only) list element from this output. The resulting vector should be length 35, corresponding to each of the 35 scary movies.
Solution
# Solution goes here ————
Problem 7:
Create a dataframe that contains the variables Title, Year and DomesticGross. Note for this exercise, you will take the output from Problem 6 and manipulate the expression using any functions introduced in lecture. You are allowed to have a hacky solution in this problem part. Once the dataframe is constructed, display the entire IMBD Scary Movie data.
Solution
# Solution goes here ————
Problem 8:
Construct a simple scatter plot showing Domestic Gross versus Year. Note that you will have to convert all vectors of character strings into numeric variables. Express DomesticGross in millions to make the plot more readable.
Solution
# Solution goes here ————
Part III Basic Exploratory Analysis
Data description
The data was extracted from the 1974 Motor Trend US magazine, and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models). Note that this dataset is automatically in R’s global environment.
head(mtcars)
|
## |
mpg |
cyl |
disp |
hp |
drat |
wt |
qsec |
vs |
am |
gear |
carb |
|
## Mazda RX4 |
21.0 |
6 |
160 |
110 |
3.90 |
2.620 |
16.46 |
0 |
1 |
4 |
4 |
|
## Mazda RX4 Wag |
21.0 |
6 |
160 |
110 |
3.90 |
2.875 |
17.02 |
0 |
1 |
4 |
4 |
|
## Datsun 710 |
22.8 |
4 |
108 |
93 |
3.85 |
2.320 |
18.61 |
1 |
1 |
4 |
1 |
|
## Hornet 4 Drive |
21.4 |
6 |
258 |
110 |
3.08 |
3.215 |
19.44 |
1 |
0 |
3 |
1 |
|
## Hornet Sportabout |
18.7 |
8 |
360 |
175 |
3.15 |
3.440 |
17.02 |
0 |
0 |
3 |
2 |
|
## Valiant |
18.1 |
6 |
225 |
105 |
2.76 |
3.460 |
20.22 |
1 |
0 |
3 |
1 |
names(mtcars)
## [1] “mpg” “cyl” “disp” “hp” “drat” “wt” “qsec” “vs” “am” “gear” ## [11] “carb”
Problem 9:
Create a single Base R plot that includes three variables. You have total flexibility in this exercise. You must include three (or more) variables to receive full credit. Points will be rewarded for aesthetics and creativity.
# Solution goes here ————
