EC201: Microeconomic Principles 1
Section A: Answer ALL questions (25 marks each). 微观经济原理代考
1
An industry consists of many firms, each with a marginal and average cost of 4. The demand for the good produced by the industry is Q = 12− ½ p where p is the industry price.
(a) What is the price and what is the quantity sold if the industry is perfectly competitive? How much profit do firms in the industry make? Illustrate your answer using a diagram.
(b) Suppose now the firms in the industry are taken over by a single monopolist. What quantity is sold at what price? How much profit does the monopolist make? How can you measure the loss to consumers from the monopolization of the industry? What is the numerical value of the loss? If all the consumers of the good are shareholders in the monopoly do they gain or lose from the monopolization of the industry?
2 微观经济原理代考
(a) A firm has a total cost function C (q) = 50 + 2q2. Find algebraic expressions for the average total cost, marginal cost and average variable cost associated with this total cost function and show the functions in a graph.
(b) Assume that there are 100 identical profit maximizing price taking firms in an industry. Each firms has a cost function C (q) = 50 + 2q2. There is no possibility of entry or exit. Assume also that the fixed cost of 50 is sunk for these firms. What is the supply of a firm as a function of the industry price? What is supply by the industry QS as a function of the industry price? If industry demand is given by Q = 5000 − 25p what is the industry price? What quantity is produced? Which is greater, price or average variable cost. Do the firms make economic profits?
(c) Define entry and exit equilibrium. Assume that entry becomes possible. Assume that for the 100 firms already in the industry the fixed cost is sunk so is not an opportunity cost. However if firms wish to enter the industry they have to pay the fixed cost. of 50. What happens to the industry price, the quantity of the good produced, the number of firms in the industry, and the profits of each firm?
3 微观经济原理代考
Consider a two-good exchange economy inhabited by two consumers with non-satiated preferences. There are no externalities. Let y be a GCE allocation with the property that each consumer gets a positive amount of each good.
(a) Could a social planner find feasible transfers t such that at least one consumer is better off under y + t than under y? Explain.
(b) Could a social planner find feasible transfers t such that both consumers are better off under y + t than under y? Explain.
4
A consumer maximises non-satiated utility with a goods endowment that comprises a positive quantity of each of two goods.
(a) Is it possible that when the price of all goods doubles, the consumer chooses to consume half as much of each good? Explain.
(b) Suppose that the consumer has Cobb-Douglas utility u(x, y) = x½ y½ . Could it be that at prices p, she demands (5, 4) and at prices 2p she demands (2, 8)? Explain.
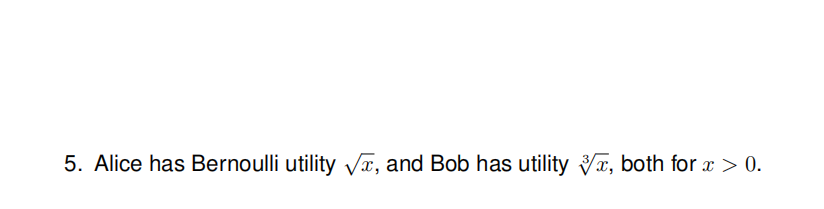
(a) Is either Alice or Bob more risk averse than the other (for x > 0)? Explain.
(b) Consider a lottery that pays 10 with probability ¼ , 20 with probability ¼ , 30 with probability ¼ , and 40 with probability ¼. What is the lottery’s expected value? Does Alice prefer the lottery to receiving 26 with certainty? What about Bob?
6
Workers are either social or studious. A firm gets a marginal revenue product of 5 from hiring a studious worker and 3 from hiring a social worker. The firm does not know the worker’s type, and initially believes that both types are equally likely. The firm then observes whether the worker attends university. The cost of attending university is 2 for both types of worker. The market for workers is competitive, so that that the firm pays every worker the firm’s expectation of the worker’s marginal revenue product.
(a) Is there a pooling equilibrium in which both types of worker attend university and are hired at a wage of 4?
(b) Is there a pooling equilibrium in which both types of worker do not attend university and are hired at a wage of 4?
Section B: Answer all THREE questions. Each question carries 50 marks. 微观经济原理代考
The major problem people had with question 7 was failing to think about the link between the different parts. See the discussion of part d.
7
There are two firms, 1 and 2. Firm 1 is a monopoly producer of good 1, producing quantity q1 at price p1. Firm 2 is a monopoly producer of good 2, producing quantity q2 at price p2.
Demand for goods 1 and 2 is
q1 = 18 − 2p1 − p2
q2 = 18 − p1 − 2p2.
Both firms produce with a constant average and marginal cost of 1.
(a) Explain the distinction between substitutes and complements. Give examples of substitutes and complements. Are goods 1 and 2 substitutes or complements?
(b) Assume that the firms play a Bertrand Nash game in which each firm chooses its price and its objective is the maximization of its own profits. What prices will be charged in the equilibrium of the game and how much of each good will be sold?
(c) Now suppose that the two firms agree that they will both set the same price, and will set the price at a level which maximizes their joint profits. What price will they set and what quantity will each firm produce?
(d) If you did the calculation correctly you will find that the price charged by the merged firm is less than the price in the Bertrand Nash game. Contrast this with the standard Cournot model in which both firms produce the same good and if the firms merge the price is higher than in the Cournot Nash game. Give a brief intuitive discussion of why the two games give different results.
8 微观经济原理代考
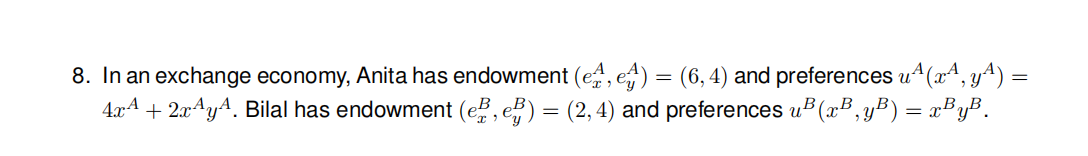
(a) 8 marks Draw the Edgeworth Box that represents this exchange economy. For each person, draw at least two indifference curves, one passing through the endowment and one through his or her origin. Clearly label your diagram.
(b) 12 marks Find Anita’s demand for the two goods.
(c) 8 marks Find Bilal’s demand for the two goods using any method you like.
(d) 8 marks Find the general-competitive-equilibrium price ratio.
(e) 8 marks Could the allocation that gives Anita and Bilal each 4 units of good x and 4 units of good y be a general-competitive-equilibrium allocation after some feasible transfers? Explain.
(f) 6 marks Write an equation for the contract curve solely in terms of xA, yA and constants. Do not waste time trying to simplify your equation.
9 微观经济原理代考
100 consumers have utility-of-wealth functions u(w) = √w, for wealth w > 0. Each consumer begins with a wealth of w = 2500, may lose 900 in an accident, and maximises expected utility. Risky consumers have the accident with probability ½. Safe consumers have the accident with probability ¼. Each consumer knows her riskiness level. A risk-neutral competitive insurance company does not know the consumers’ riskiness levels but knows that exactly 50 are risky and 50 are safe.
(a) 12 marks What would the risky type’s expected utility be if he bought full insurance at a price that is actuarially fair for him? What would be the insurance company’s expected profits by selling him such insurance?
(b) 14 marks Explain the meaning of a pooling equilibrium in a setting with asymmetric information. Is there a pooling equilibrium in the perfectly competitive insurance market with free entry and exit in which the insurance company offers full insurance against the loss of 900 for a premium of ½ (½ + ¼ ) 900 = 337.5 and all consumers accept? Explain.
(c) 12 marks Explain whether there is a separating equilibrium in the perfectly competitive insurance market with free entry and exit in which the insurance company offers two types of contract: full insurance at a cost of ½ 900 = 450 and partial insurance that covers 800 at a cost of ¼ 800 = 200.
(d) 12 marks Treating the insurance company as a risk-neutral person, describe an outcome in this market that maximises the utilitarian social-welfare function.

