MATH 7241: Problems for Notes #1
数学作业代写代做 Reading: relevant background material for these problems can be found in the class notes, and in Ross (Sections 2.1 2.2, 2.3, 2.4) and in Grinstead
Reading: relevant background material for these problems can be found in the class notes, and in Ross (Sections 2.1 2.2, 2.3, 2.4) and in Grinstead and Snell (Chapters 1,2 3, 6).
Exercise 1 数学作业代写代做
You have two coins, one is unbiased, the other is biased with probability of Heads equal to 2/3. You toss both coins twice, X is the number of Heads for the fair coin, Y is the number of Heads for the biased coin. Find P(X>Y ).
Exercise 2
Let A and B be events such that P(A)=0.7 and P(B)=0.9. Find the largest and smallest possible values of P(A ∪ B) − P(A ∩ B) (note: the event A ∪ B means either A or B or both are true, the event A ∩ B means both A and B are true).
Exercise 3 数学作业代写代做
A town has five hotels; three people arrive and each randomly and independently selects a hotel. Find the probability that exactly two of them stay in the same hotel.
Exercise 4
Find the mean and variance of the geometric distribution:
P(X = n) = (1 − p)n−1 p, n = 1, 2,…
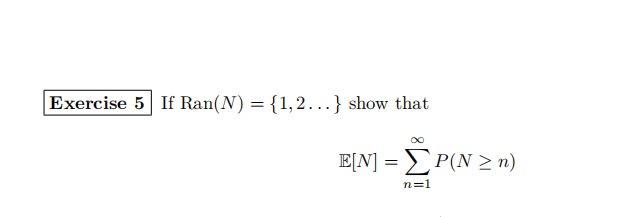
Exercise 6 数学作业代写代做
Randomly distribute r balls in n boxes. Find the probability that the first box is empty. Find the probability that the first two boxes are both empty.
Exercise 7
The current in a resistor is a random variable X. The pdf of X is f(x) = e−(x−1) for x ≥ 1. The power dissipated in the resistor is Y = X2. Find the pdf of Y .
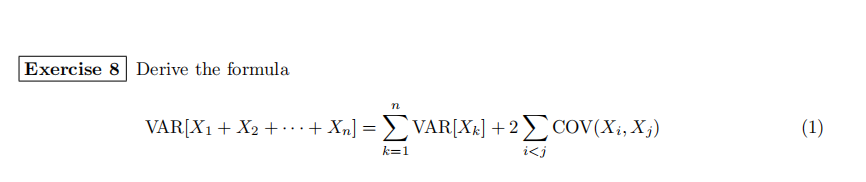
Exercise 9
We start with a stick of length 1, and break it in two pieces at a randomly chosen position (chosen uniformly over its length). Find the mean and variance of the longer piece.

Exercise 11 数学作业代写代做
In class we considered this problem: “An urn contains n Red balls and m Black balls. Suppose that k balls are withdrawn from the urn, and let X be the number of Red balls among these. Find E[X] assuming (i) replacement, and (ii) no replacement.” Using the same reasoning as in class, compute VAR[X] assuming (i) replacement, and (ii) no replacement. [Hint: use the formula from Exercise 8 above. The answers will be different for the two cases].

