Math 541 Practice for Mid Term
数学期中练习代写 Remarks.Answer ALL the questions below. Definition (subsections (a)) is just a definition and there is no need to justify it. So just write it
Remarks.
- Answer ALL the questions below.
- Definition (subsections (a)) is just a definition and there is no need to justify it. So just write it down.
- It is recommended that answers to subsections (b) and (c) are written in the followingformat:
0) If it is a computation start by writing the answer.
i) Main points that will appear in your explanation or proof or
ii) The actual explanation or proof or computation.
1.Linear algebra. 数学期中练习代写
(a) (3) Suppose V is a finite dimensional vector space over R, with an inner product〈,〉. For a subspace W ⊂ V , define its or thogonal complement W⊥ ⊂ V .
(b) (7) Explain what does it mean for vectors w1,… ,wm ∊ W, to be orthogonal basis.
Use such basis to show that:
- dim(V) = dim(W) + dim(W⊥):
- V = W⊕W⊥, where⊕denotes direct sum of two spaces.
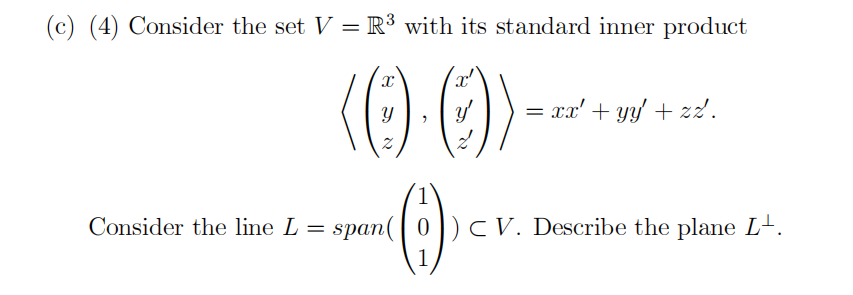
2.Notion of a group. 数学期中练习代写
(a) (3) Define the notion of a group.
(b) (7) Let V be a vector space over a field F. Show that
GL(V ) = {T : V → V ; such that T is invertible linear transformationg},
is in a natural way a group, with the operation of composition of linear transformation, and with identity the map IdV(v) = v; for every v ∊ V .
(c) (4) Consider the finite field F2 = {0,1}, with its standard addition + and multiplication ∙ . Consider the group (with respect to matrix multiplication),
G = GL2(F2) = {A ∊ M2(F2); A is invertibleg}.
Write down the multiplication table of G. In particular, deduce that G = GL2(F2) is a non-commutative group, i.e., find A,B 2 G such that AB ≠ BA.
3.Notion of subgroup. 数学期中练习代写
(a) (3) Suppose G is a group, and H ⊂ G, a subset. Define when we say that H is a subgroup of G.
(b) (7) Show that for a subset H ⊂ G, where G is a group, the following two conditions are equivalent:
- H < G;
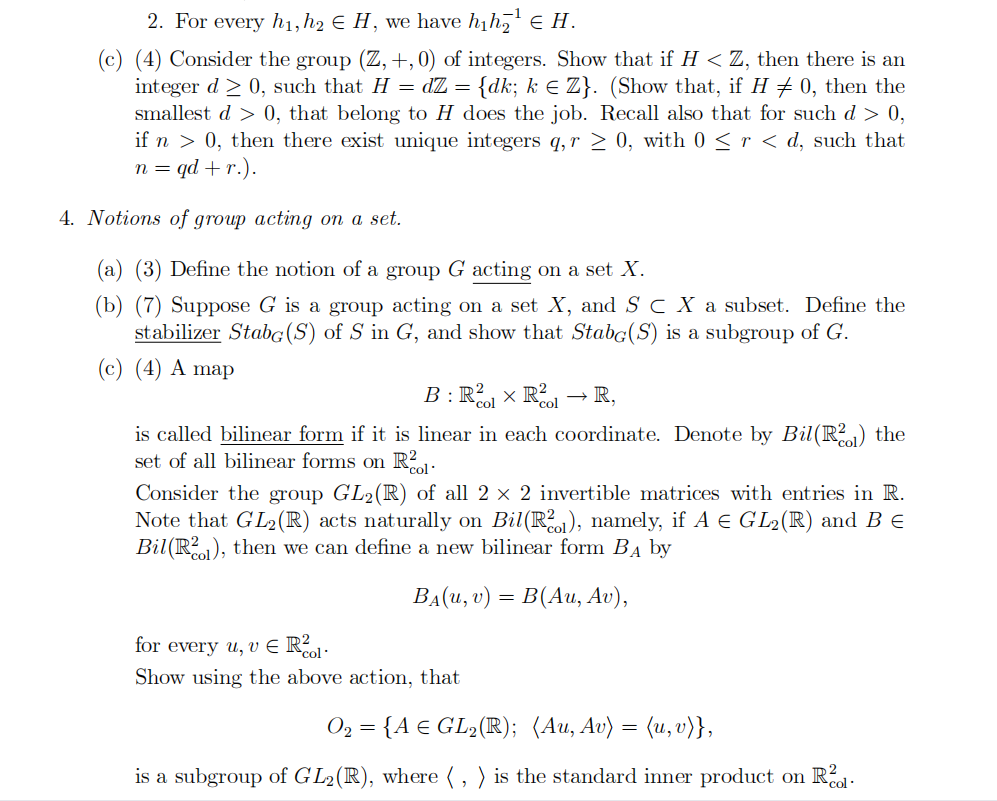
5.The orthogonal group O2.
(a) (3) Define the orthogonal group O2 < GL2(R).


7.Notions of homomorphism. Suppose G and H are groups. 数学期中练习代写
(a) (3) Define when a map φ : G → H is an homomorphism.
(b) (7) Suppose φ : G → H is an homomorphism. Consider the collection
Im(φ) = {φ(g) ∈ G; g ∈ G} ⊂ H,
called the image of φ, and the collection
Ker(φ) = {g ∈ G; φ(g) = 1H} ⊂ G,
called the kernel of φ.
Show that Im(φ) is a subgroup of H, and Ker(φ) a subgroup of G.
(c) (4) Denote by C* the collection of all non-zero complex numbers. It is a group under usual multiplication · of complex numbers. In addition consider the collection R of real numbers. It is a group under the usual addition + of real numbers.
Consider the mapping
φ : R → C* ,
given by φ(θ) = e2πiθ = cos(2πθ) + isin(2πθ), for θ ∈ R.
- Show that φis homomorphism.
- Show that Ker(φ) = Z and Im(φ) = S1= {z ∈C*; ∣z∣ = 1} the unit circle in the plane.

