Applied Statistics (ECS764P) – Lab 1
代写应用统计作业 Plot this distribution (in Python or on a piece of paper). Compute its CDF. Use your plot to check that your answer makes sense.
1 Theory 代写应用统计作业
The following questions are meant to test your understanding of lectures 1 and 2. Answers to these questions will not be marked, but if you can solve these questions, you will be fifine at the exam…
1.The triangular distribution is the distribution you get by summing two uniform distributions on [0, 2]. Its PDF is given by:
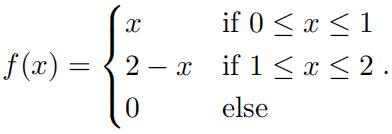
Plot this distribution (in Python or on a piece of paper). Compute its CDF. Use your plot to check that your answer makes sense.
2.Consider the array [3,4,2,5]. Find the sample mean and the sample median. Suppose we add an additional observation x ≥ 5 to this array. What is the smallest value of x for which the mean will be larger or equal to the median?
3.Compute the following:
(a) Consider the slightly modifified Bernoulli distribution which is supported by {1, 2} (instead of {0, 1})and where the probability mass of {1} is (1 − p) and the probability mass of {2} is p. Compute the variance of this distribution.
(b) The mean of the triangular distribution defifined above.
(c) The standard deviation of the uniform distribution on an interval [a, b],
4.Recall that measures (and therefore probability measures) are σ-additive. This means that if µ is a measure, X is a set, and (Ai)i∈N is a collection of disjoint subsets which partition X – that is to say
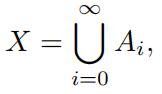
then it must be the case that
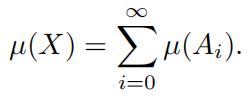
(1)
In other words, the masses of the set Ai add up to the mass of X.
Consider the uniform distribution on (0, 1]. What is its PDF? Consider the collection of sets defifined by
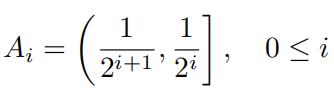
Show that it forms a partition of (0, 1] (i.e. the Ais are pairwise disjoint and their union is the whole of (0, 1]. Show that the σ-additivity equation (1) holds for this partition. (Hint: You might want to check out this page: https://en.wikipedia.org/wiki/Geometric_series.)

2 Practice 代写应用统计作业
General instructions Complete the following tasks by creating a Jupyter Notebook. This Jupyter Notebook will need to be submitted on QMPlus (follow Labs and Coursework→ Coursework 1 – submission) by 20 October 2022 at 11:00. This coursework will count for 10% of your fifinal mark for the module.
The marks awarded for each sub-question are detailed below. However, note that your code must run without any bugs to get full marks. The person marking your worksheet will start by running all cells. If any error is thrown, your fifinal grade will be halved (i.e. the maximum possible grade for a buggy notebook will be 5/10).
There is not ‘a correct way’ to answer these questions!
1.(1 mark) Import the UN’s Population Growth, Fertility and Mortality Indicators from http://data.un.org/_Docs/SYB/CSV/SYB64_246_202110_Population%20Growth,%20Fertility%20and%20Mortality%20Indicators.csv 代写应用统计作业
2.(2 marks) Select the life expectancy data for both sexes (years) series for countries only (i.e. remove region/continent-wise data), you can choose to select one year of data only (e.g. 2020), or to collect the data for all years. Format this data as a numpy array for processing. Print the size N of your dataset.
3.(2 marks) Plot a histogram of the data, add vertical lines for the mean and median of the data. Comment brieflfly on what the values of the mean and the median tell us about the distribution of the data.
4.(2 marks) Compute and display the range, the interquartile range, and the standard deviation σ. Plot a histogram of the data with vertical lines the fifirst quartile, the third quartile, and the mean +/− the standard deviation (i.e. 4 vertical lines in total).
5.(3 marks) We covered several classes of distributions in the lecture (e.g. distributions on fifinite sets).
Based on your observations so far, which class and which distribution within this class do you think would be suitable to model life expectancy? Brieflfly justify your choice. Generate N samples from this distribution. Adjust your parameters so that these samples are not too dissimilar to those from the life expectancy data. Plot a histogram for this data together with vertical lines for the mean, fifirst, second and third quartile.

更多代写:美国Online exam代考 澳洲pte代考 商科Midterm代考 澳洲culture essay代写 UNSW大学论文代写 代写为什么会被发现
