Mathematics
代考Mathematics This mark can be given if the discriminant is seen as part of the formula normally used for solving a quadratic equation.
Notice to Markers
Significant Figures:
All correct answers should be rewarded regardless of the number of significant figures used, with the exception of question 5. For this question, 1 discretionary mark is available which will only be awarded to students who correctly give their answer to the number of significant figures explicitly requested.
Types of marks awarded:
There are three types of mark:
M = Method (In the event of a correct answer, M marks can be implied unless the M mark is followed by * in which case, the working must be seen.)
A = Answer
B = Correct answer independent of method
Please note that A marks cannot be scored if the M marks have not been earned (i.e. M0 followed by A1 is not possible) unless there is a special case allowing this which will be indicated in the mark scheme. If a candidate obtains full marks or no marks in a section, it is only necessary to enter the score on the script. If there is a part score, then each mark scored must be shown as M1, A1 or B1 on the script.
Error Carried Forward (ECF): 代考Mathematics
If a candidate makes a numerical error in a calculation, and the answer is used in asubsequent part of the question, the marking procedure is as follows. If the candidate’s working shows a method which is clearly correct, then the M marks can still be awarded (and ‘ECF’ should be written on the script) but no A marks are available. The only exception to this is when there is a follow through permitted. This is denoted by A1ft and B1ft – and allowing a follow through will usually be indicated in the mark scheme as well. 代考Mathematics
If a student has crossed out an answer, it should be always disregarded – even if it is correct.
Misreads:
Where a candidate incorrectly copies information from a question this may be marked as a misread using the annotation MR. In this case a one mark penalty should be applied and all other marks (including A marks) may be awarded for error carried forward. Markers should use discretion to award fewer marks if the question becomes much simpler because of the misread. If an inappropriate result is reached as a result of the misread (eg cos Ө = 2 or a probability greater than 1) the final A mark(s) should not be awarded. Any misread cases which are unusual or difficult to mark should be highlighted in the Marker Report.
Where a candidate miscopies their own work this is an error NOT a misread.IFY Mathematics
Question 1
(a) (𝑎𝑥 ± 𝑏)(𝑐𝑥 ± 𝑑) where 𝑎𝑐 = 18 and 𝑏𝑑 = −20 [M1]
(3𝑥 + 4)(6𝑥 − 5)[A1]
(b) Finds discriminant (−8). Some evidence must be seen as it is a ‘show that’ question. Just quoting −8 is good enough, but just saying ‘the discriminant is negative’ without any working is not sufficient. This mark can be given if the discriminant is seen as part of the formula normally used for solving a quadratic equation.[M1*]
This is negative, so there are no real roots.[A1]
Question 2
Uses cosine formula [322 = 282 + 302 − 2 × 28 × 30 × cos 𝜃] [M1]
Rearranges [M1]
or equivalent but must be in this form.[A1]
Question 3
(a) 6𝑝2 [B1]
(b) 1 − 3𝑝[B1]
(c) Writes 2𝑝 × their (1 − 3𝑝) = 
and forms the quadratic equation [B1]
300𝑝2 − 100𝑝 + 3 = 0
Attempts to solve the equation. [Please note this is not dependent on the previous B mark] [M1]
𝑝 = 
or equivalent. Accept answers rounding to 0.0333 [A1]
Question 4 代考Mathematics
(a) Finds gradient of AB (=
) [M1]
Correct follow through equation in any form e.g. 𝑦 − 11 = their (𝑥 − 4) [M1]
3𝑥 − 4𝑦 + 32 = 0 or equivalent but must be in this form.[A1]
(b) Substitutes 𝑥 = 12 and 𝑦 = 17 into their equation and confirms that it comes to zero, or any other valid method; followed by a minimal conclusion:‘QED’ or just a tick is sufficient.[M1*]
(c) Finds the length of BC (= 10) [M1]
Reaches a correct follow through equation in any form
e.g. (𝑥 − 12) 2 + (𝑦 − 17) 2 = their 𝐵𝐶2 [M1]
𝑥 2 + 𝑦 2 − 24𝑥 − 34𝑦 + 333 = 0 (Must be in this form)[A1]
Question 5
(a) Some evidence needs to be seen e.g. 120 + 10 × −3 followed by 90 [M1*]
(b) 0 = 
[240 − 3(𝑛 − 1)] [M1]
Solves. This is dependent on the previous M mark. [M1]
𝑛 = 81 [A1]
(c) Establishes first term (= 120) and common ratio ( =)
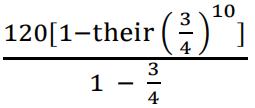
[M1]
= 452.9695… (can be implied) [A1]
= 453.0 to 4 significant figures. Do not accept 453. Allow follow through
provided a more accurate answer is seen earlier. [A1ft]
Question 6
(a) Uses sine formula 
[M1]
(A1) for each. [A3]
Allow any alternative correct answer but it must be in surd form.
(b) Correct order of solving (divides by 2,takes square root, then arcsin) seen or implied anywhere [M1]
Sight of ± (can be implied from correct solutions)
(A1) any two correct; (A2) all correct [B1]
One mark is lost for any extra solutions in the range. Ignore solutions
outside the range.[A2]
Question 7
(a) 4𝑝 − 2𝑞 = 30; 9𝑝 + 3𝑞 = 15 or equivalent (B1) for each [B2]
(b) Please note: all working must be shown. [M1*]
Evidence of finding one unknown [M1*]
Evidence of finding second unknown [A1ft]
Allow follow through on their equations [A1ft]
(c)
Question 8
(a) 
[B1]
(b) Finds gradient (= 4) and writes down a correct follow through equation in any form e.g. 𝑦 + 4 = their 4(𝑥 − ln 2) or writes 𝑦 = their 4𝑥 + 𝑐 and finds a value for 𝑐. [M1]
𝑦 = 4𝑥 − 4(ln 2 + 1) Accept only in this form.[A1]
(c) Replaces LHS with exponentials, sets equal to 12 and reaches a quadratic
equation in 𝑒x[𝑒2x + 2𝑒x− 8 = 0] [M1]
Solves. This is dependent on the previous M mark. [ 𝑒x = −4, 2]
𝑥 = ln 2 [This must be in exact form. If any attempt is made to solve 𝑒x =−4 without discarding, this mark is lost.][A1]
Question 9
(a) 6C2× 104× 𝑚2 (M1) 6C4× 102 × 𝑚4 (M1) Accept equivalent binomial coefficients, allow presence of 𝑥 but do not accept reversed powers. [M2]
Multiplies second by 625 or divides first by 625 and solves [there must now be no 𝑥 present] [M1]
or equivalent. Both answers needed. [A1]
Please note: following the syllabus change, if the binomial coefficients are written the wrong way round, this is no longer penalised.
(b) 𝑎𝑟 + 𝑎𝑟3 = 78; 𝑎𝑟2 + 𝑎𝑟4 = 117 [M1]
Spots the connection [117 = 78𝑟] and finds a value for 𝑟 [M1]
Substitutes their 𝑟 into either equation and finds a value for 𝑎. [M1]
𝑎 = 16, 𝑟 =
or equivalent. (Both needed) [A1]
Question 10 代考Mathematics
(a) Attempts to differentiate (sight of 𝑥2 , 𝑥 or 𝑘 is sufficient for this mark)
[3𝑥2 + 2ℎ𝑥 + 𝑘] [M1*]Attempts to differentiate a second time (sight of 𝑥 or the coefficient of the 𝑥 −term of their 
is sufficient for this mark) [6𝑥 + 2ℎ] [M1*]
Substitutes 𝑥 = 5 into both expressions [75 + 10ℎ + 𝑘, 30 + 2ℎ] and sets both equal to 0. [M1]
ℎ = −15, 𝑘 = 75 (A1) for each [A2]
(b) Attempts to integrate (sight of 𝑥3 , 𝑥2 or 𝑥 is sufficient for this mark). This mark is not lost if the constant is missing, but this is the only mark that can be scored. [M1*]
(𝑦 = ) 2𝑥3 − 7𝑥2 + 5𝑥 + 𝑐 Correct answer [A1]
Substitutes 𝑥 = 3 and 𝑦 = 1 into equation and finds a value for 𝑐 (= −5) [M1]
𝑦 = 2𝑥3 − 7𝑥2 + 5𝑥 − 5 (Please note 𝑦 = ⋯ must be present)[A1]
Question 11
(a) Please note: this is a ‘show that’ question so all working must be seen.
Attempts to differentiate (sight of 𝑥 or − 4 is sufficient for this mark) [2𝑥 − 4] [M1*]
Finds gradient when 𝑥 =(= −1), inverts and changes sign (= 1) [M1*]
Correct follow through equation in any form e.g. 𝑦 −
= their 1(𝑥 −) or writes 𝑦 = their 1(𝑥) + 𝑐 and finds a value for 𝑐 [M1*]
Reaches 𝑦 = 𝑥 −
having scored all 3 M marks and no errors seen. [A1]
Question 11 – (continued)
(b) Attempts to find area under the curve by integrating (sight of 𝑥3 , 𝑥2 or 𝑥 is sufficient for this mark) [ 
− 2𝑥 2 + 5𝑥] [M1*]
Question 12
Reaches result after at least one intermediate line of correct working
(Both M marks scored and no errors seen)
Question 12 – (continued)
(b) In this part, allow the marks if a different version of 𝑉 has been used
e.g.
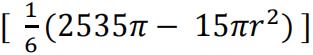
Attempts to differentiate (sight of 2535𝜋 or 𝑟 2 is sufficient for this mark)[M1*]
Sets equal to 0 (can be implied) [M1]
Reaches 𝑟2 = ⋯ ( 169) [M1]
𝑟 = 13 (cm) [A1]
Attempts to differentiate a second time (sight of 𝑟 is sufficient for this mark) [M1*]
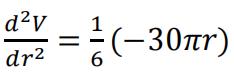
[A1]
This is negative, so there is a maximum. (Allow follow through on their 
[A1ft]
provided it gives a maximum.)
or Takes a numerical value between 0 and 13 and shows 
(M1*)
Takes a numerical value above 13 and shows (M1*)
Thus there is a maximum when 𝑟 = 13 (A1ft) Allow follow through on their 
provided it gives a maximum.
(c) 
terms of 3 𝜋 (cm3 ) Accept anything rounding to 3660𝜋. The answer must be in 𝜋. Allow follow through on their 𝑟. [B1ft]
Question 13
a) 8 [B1]
(b) Applies power law and combines logs correctly (seen anywhere) [M1*]
Removes logs correctly and at the right time (seen anywhere) [M1*]
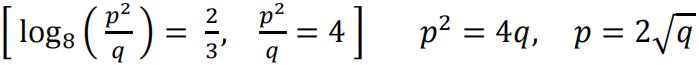
[A1]
Replaces 𝑝 with their 
or 𝑞 with their function of 𝑝 [M1]
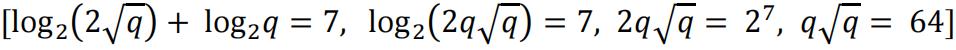
𝑝 = 8, 𝑞 = 16
[(A1) for one answer correct; (A1ft) for second answer correct] [A2](c)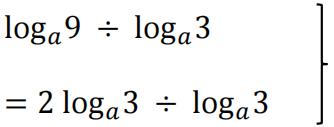 
Both of these steps must be seen.[M1*]
[M1*]
= 2 (Both M marks scored and no errors seen) [A1]
更多代写：Online exma代写 托福在家考作弊 Matlab代写推荐 HK英语论文代写 essay论文润色修改 Zoom作弊
