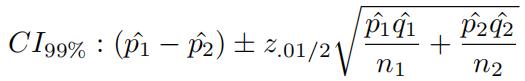APPM 4570/5570
Homework #5
STAT 4000/5000
代写统计作业 Back to ladybugs – recall that aphid infestation of fruit trees is usually controlled either via pesticides or via ladybug innundation.
Problem 1
Please do problem #37 in here. In addition to answering the parts (a) and (b), answer the following:
c) Construct the 95% confifidence intervals for the indoor and for the outdoor true concentration. d) Do these CIs overlap, and can you use that fact to test the hypothesis test in part (a)? Why or why not? Write a paragraph justifying your answer. To help you think through this answer, use the following short paper.
(a) Calculate a confifidence interval for the population mean difffference between indoor and outdoor concentrations using a confifidence level of 95%, and interpret the resulting interval. 代写统计作业
The confifidence interval is given by:
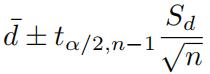
and in R we have the mean difffference between indoor and outdoor d ¯ is -0.42, the standard deviation Sd = 0.39, and t0.05/2,33−1 = -2.04. Therefore, the 95% CI is (-0.42 ± 0.14) ng/m3 . This 95% CI is a range of values that you can be 95% certain contains the true mean difffference between indoor and outdoor concentration of the chemical.
(b) If a 34th house were to be randomly selected from the population, between what values would you predict the difffference in concentrations to lie?
The new house concentration difffference is a new random variable, X34, whose distribution will be centered at the true mean difffference, with variance σ 2d. So we can express this as X34 = µd + ε, where ε ∼ N(0, σ2). However, we don’t know the true difffference µd – we estimated it using d ¯ in part (a) as-0.42ng/m3. So,
V ar(X34) = V ar(d ¯+ ε) = σ 2d(1 +1n ),
which is estimated as Sd 2 (1 +1n ). So, the central 95% probability interval will be given as:
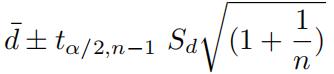
(c) The 95% confifidence intervals for the indoor and for the outdoor concentration. Similar to part (a), we need to fifind the 95% CI for the indoor and for the outdoor concentration separately. And an easier way to do in R is to use “t.test”.
(d) These CIs don’t overlap, and we can use that fact: We would reject the null hypothesis that there is no difffference between indoor and outdoor concentrations, in favor of the two-sided alternative that there is, at 5% signifificance.
Problem 2 代写统计作业
Back to ladybugs – recall that aphid infestation of fruit trees is usually controlled either via pesticides or via ladybug innundation. In a particular area, 2 difffferent (and well isolated) groves, with 15 fruit trees each, are selected for an experiment. The trees in both groves are of the same age, roughly the same size,and can be assumed to be independent. One grove is sprayed with pesticides, and one is flflooded with ladybugs. The fruit yield (in pounds) for each tree is given below:
Pesticide trees: 55.57109 36.50319 47.80090 33.34822 36.16251 35.28337 41.50154 44.18931 40.81439
33.88648 44.90427 49.97089 22.85414 27.84301 38.49843
Ladybug trees: 45.44505 35.52320 46.97865 45.76921 41.66216 54.69599 58.77678 49.08538 48.53812
70.17137 51.86253 39.59365 42.10194 47.39945 39.04648
(a) Test to see if each of these two samples come from a normal distribution (need not be the same normal distribution). Use signifificance level of 5%.
The p-value for Pesticide is 0.9844, and the p-value for Ladybug is 0.6941, which are much larger than 0.05. So, we fail to reject the two null hypotheses, which means these two samples are normally distributed. 代写统计作业
(b) Find the sample means of yields for the two groves, and provide the two 95% confifidence intervals for the true mean yields for trees under the two treatments.
Assume these two samples are normally distributed. Use “t.test” to fifind the sample means and the 95% CI for the true mean, we can obtain from R: From the results, we can know that the sample mean for Pesticide is 39.28, and the sample mean for Ladybug is 47.78. And the 95% CI for the true mean for Pesticide is (34.56, 43.99), for Ladybug is (42.95, 52.60).
(c) Find the sample variances for the yields in the two groves.
Directly use “var(Pesticide)” and “var(Ladybug)” in R fifind the sample variances.
Sample variance of Pesticide = 72.44475 lb2 ,
Sample variance of Ladybug = 75.8964 lb2 .
(d) Test the equality of these two variances using signifificance level of 5%. (Write out the hypotheses,compute the test statistic, p-value, and write out the conclusion)
Hypothesis: H0 : ![]()
In an easier way, we can use “var.test” in R which performs the equality of variances test for normal data, and the result is as below. In this case, the test statistic should be the ratio of sample variances, which is 0.9545, and the p-value is equal to 0.9318. Therefore, since the p-value is large,we fail to reject the null hypothesis at a signifificant level of 5%, which means these two variances are statistically equal.
(e) Test the equality of the two mean yields. (Write out the hypotheses, compute the test statistic,p-value, and write out the conclusion)
Hypothesis: H0 : µ1 = µ2; H1 : µ1≠µ2. 代写统计作业
We can use “t.test” in R which performs the equality of means test for normal data:
t.test(Ladybug,Pesticide,var.equal=TRUE)
Two Sample t-test
data: Ladybug and Pesticide
t = 2.7033, df = 28, p-value = 0.01154
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
2.05950 14.94293
sample estimates:
mean of x mean of y
47.77666 39.27545
In this case, the test statistic should the t value, which is -2.7033, and the p-value is equal to 0.01154. Therefore, since the p-value is small enough, we can reject the null hypothesis at a signifificant level of 5%, which means these two means are statistically difffferent.

Problem 3 代写统计作业
A controlled clinical trial was run to investigate the effffect of the drug stelazine on chronic schizophrenics.
The trials were conducted on chronic schizophrenics in two closed wards. In each of the wards, the patients were divided into two groups matched for age, length of time in the hospital, and disease severity as measured by a behavior rating score. One member of each pair was given stelazine, and the other a placebo. Only the hospital pharmacist knew which member of each pair received the actual drug.The data is given in the spreadsheet and shows, for each of the patients, the change in the patient’s behavioral rating score after 3 months. Positive values indicate an improvement in the patient’s behavior over the three month period, while negative values indicate that the patient’s behavior declined. The table also shows the difffference between the stelazine patient’s change and placebo patient’s change for each of the patient pairs.
Use appropriate hypothesis tests to answer the following two questions, being sure to complete each of the four steps: i. state the two hypotheses being tested (be sure to defifine any parameters used, if they were not defifined previously), ii. compute the appropriate test statistic, degrees of freedom (if applicable), and p-value, iii. decide whether to reject the null hypothesis when using a signifificance level of 0.05, and iv. conclude by writing a short sentence explaining what your decision means in the context of the problem.
(a) Considering all patients, test whether the average behavioral change is higher for patients using stelazine than for patients receiving a placebo (thus indicating that stelazine improves chronic schizophrenic behavior).
Hypothesis: H0 : µs − µp = 0, H1 : µs − µp ≠ 0
Where µs and µp are the average behavioral changes for those taking stelazine and those taking a placebo, respectively.
First, test normality of each sample and equality of the variances to decide whether to use a pooled t test or not. 代写统计作业
Thus, we cannot reject the null hypothesis that the mean behavioral changes are equal for those on stelazine versus those taking a placebo when using a signifificance level of 0.05. We conclude that there is no difffference in behavioral changes between those taking stelazine and those taking a placebo.
(b) Using the difffferences, S-P, test whether stelazine is more effffective, on average, in one of the wards than in the other. Carry out the appropriate test for the equality of variances if necessary. Were we right to combine all patients for our answer in (a)?
Hypothesis: H0 : µA − µB = 0, H1 : µA − µB ≠ 0
Where µA and µB represent the average difffference in behavioral change between stelazine and placebo patients at ward A and ward B, respectively.
Problem 4 代写统计作业
A study performed in a Boston area high school showed a link between drinking soda and weak bones.Among 57 active children who do not drink soda, 5 suffffered fractures. Among 107 active children who reported drinking soda, 38 suffffered fractures. The study did not specify how much soda the children drank.(The Denver Post, 6/15/2000, “New study links cola, weak bones.”) 代写统计作业
(a) Using a two-sample test of proportions, determine whether this study provides signifificant evidence at the 1% level to suggest that the probability of getting a fracture is lower for kids that do not drink soda than it is for kids that do drink soda.
Hypothesis: H0 : p1 − p2 = 0, H1 : p1 − p2 < 0, α = 0.01
Where p1 is the true proportion of fractures for non-soda drinkers and p2 is the true proportion of fractures for soda drinkers.
(b) Construct a 99% confifidence interval for the difffference in the probabilities of getting a fracture for non-cola drinking and cola drinking kids. In one or two sentences, interpret this interval for someone who has never taken a statistics course.