EC220
Introduction to Econometrics
代写计量经济学作业 The answers must then be converted to pdf and uploaded to Moodle as ONE individual fifile together with the Coversheet.
Instructions to candidates 代写计量经济学作业
This paper contains FOUR questions, divided into two sections. Section A contains ONE question related to Michaelmas Term and Section B contains THREE questions related to Lent Term. You should answer ALL questions from Section A and ALL questions from Section B.
If at any point in this exam you feel that anything is unclear, please make additional assumptions that you feel are necessary and state them clearly.
For Section A: Please type your answer in a Word-processing software on a computer (e.g. Word).You could combine the typed document with scanned or photographed hand-drawn diagrams and computations. The maximum word count is 1500 words, beyond which nothing will be marked. There is no minimum word count and concise answers will be rewarded. 代写计量经济学作业
For Section B: Please use pen and paper and scan (or photograph) your answers. You could also use an iPad or a tablet. There is no maximum word count for Section B. Please annotate your answers clearly.
The answers must then be converted to pdf and uploaded to Moodle as ONE individual fifile together with the Coversheet. Please make sure every single scanned page is legible and properly ordered.
The fifile will be run through Turnitin to ensure academic integrity.
Time Allowed Submit PDF with answers within 24 hours after offificial start of the exam
Expected effort Reading Time: 15 minutes
Answering Time: 3 hours
You are supplied with:
Lindley & Scott Cambridge Statistical Tables
Table A5 Durbin-Watson d-statistic
You may also use: Open book examination
Calculators: Calculators are allowed in this exam
Section A 代写计量经济学作业
(Answer all questions.)
Question 1
[33.34 marks]
Johannes Gutenberg introduced the metal moveable type printing press, an important information technology, in Europe in the city of Mainz, Germany, in 1439. In its early stage, the printing technology was complex and semi-proprietary. The technology required skilled craftsmen and suffificient fifinancial backing. Over the coming decades, the technology spread to other cities primarily because Gutenberg’s apprentices, or their apprentices, moved elsewhere and set up their own print shops. By 1500, about 10% of the larger cities in Europe had printing presses.
Books were diffificult to transport over long distances during this period because they were heavy and could be easily damaged by rain or damp conditions. As a result, cities with printing presses benefifited from much more printed material, books and pamphlets, than cities without local presses. Among the materials printed were books about arithmetic and merchant manuals, spreading commercial knowhow and skills, like the calculation of interest rates and bookkeeping techniques, to a merchant class. We would like to know whether printing and the proliferation of modern business practices contributed to city growth, as measured by population size. The dataset consists of cities in central Europe and observations are at the city level.
Table 1 shows coeffificients from regressions of the difference in log population (city size) between different years on a dummy variable for whether the city had a printing press before 1500.
Additional regressors (no coeffificients shown) are dummy variables for whether the city had a university in 1450(University in 1450), whether it used to be a Roman site, whether it is a capital city, whether it is an Atlantic port, a Mediterranean port, a Baltic port or whether it is located on a navigable river, and log population size in 1400.
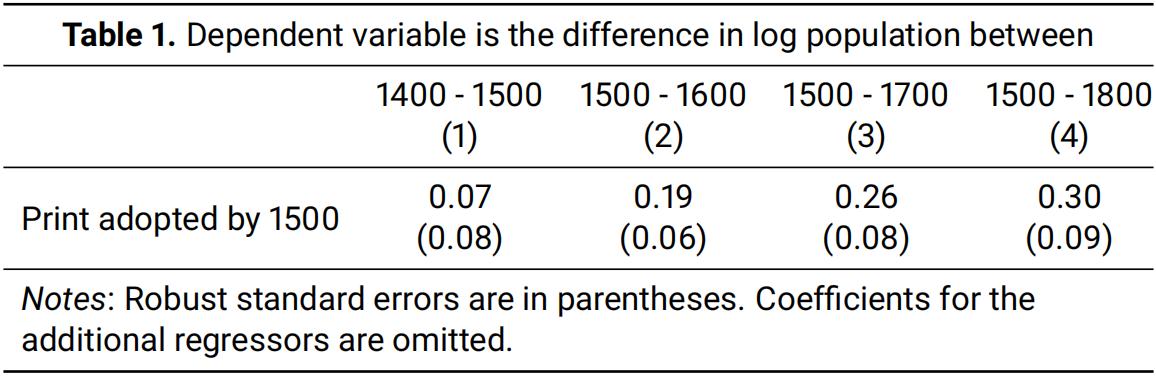
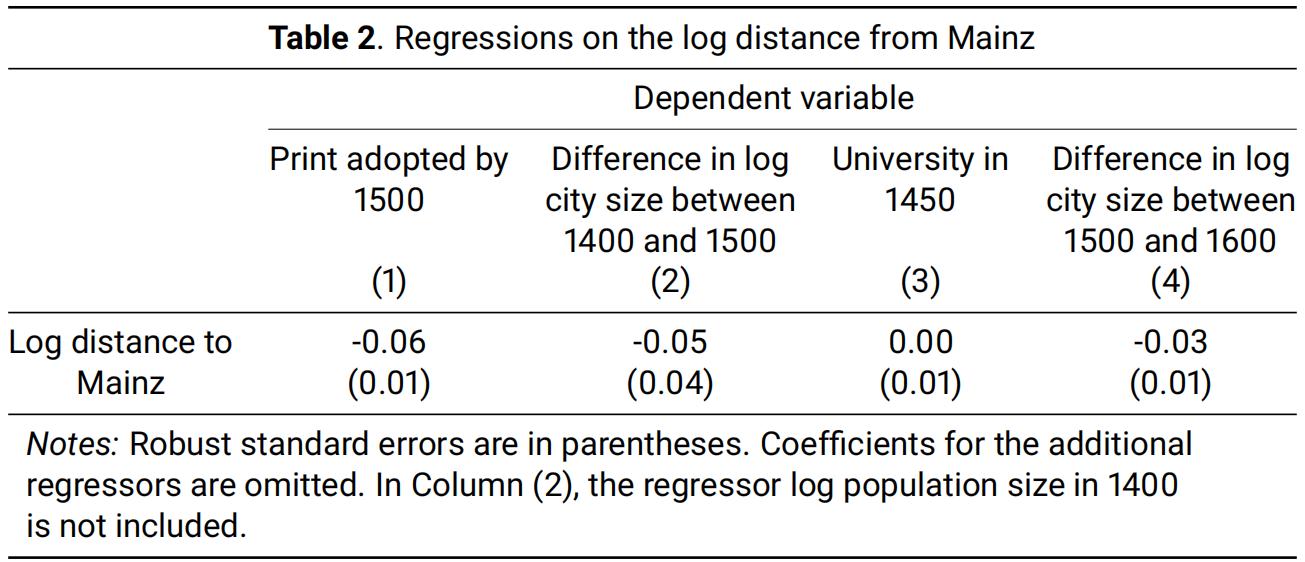
Table 2 shows regressions of various dependent variables on the log distance of the city from Mainz and the same regressors as in Table 1.
(a)Interpret the results in Table 1.
What do the results tell us whether the early adoption of printing contributed to city growth? Discuss whether you could interpret the results causally.[9 marks]
(b)Explain whether you would also include a variable for the number of editions (output) printed per capita during 1450-1500 as a regressor in the regressions in Table 1 in order to study the causal effect of printing on city growth.[5 marks]
(c)Using the provided information, explain whether the distance from Mainz, where printing was invented, would be a good instrument for the adoption of print before 1500.[9 marks] 代写计量经济学作业
(d)What is the instrumental variables estimate of print adoption before 1500 on the difference in log city size between 1500 and 1600 using log distance from Mainz as an instrument? Explain
how you arrive at your result. Comment on the difference to the corresponding OLS result.[8 marks]
(e)A researcher obtains the residuals from the OLS regression in Column (1), Table 2, and regresses the residuals on the variable Log distance to M ainz and the other regressors. Calculate the Rsquared of this new regression. Carefully explain what additional information you would require if you cannot make such a calculation.[2.34 marks]

Section B 代写计量经济学作业
(Answer all questions.)
Question 2
[22.33 marks]
Consider the following bivariate regression model without intercept
![]()
for i = 1, . . . , n. We impose the following assumptions.
SLR.1 The population model is y = βx2 + u.
SLR.2 We have a random sample of size n, {(yi , xi) : i = 1, . . . , n}, following the population model in SLR.1.
SLR.3 The sample outcomes on {xi : i = 1, . . . , n} are not all the same value.
SLR.4 The error term u satisfifies E(u|x) = 0 for any value of x.
(a)Let βˆ be the OLS estimator for the regression from y on x 2 (without intercept). Show that βˆ is consistent for β under SLR.1-4.[3 marks]
(b)Under SLR.1-4, derive the (conditional) variance V ar(βˆ|X), where X = (x1, . . . , xn).[3.33 marks]
(c)Propose an estimator for V ar(βˆ|X) under SLR.1-4, and explain how you can use it to test the hypothesis H0 : β = 5 against H1 : β ≠ 5. Clearly state any assumptions you are making.[4 marks] 代写计量经济学作业
(d)Now consider the OLS estimator β˜ for regressing y on x without an intercept. Derive the (conditional) expectation E(β˜|X) under SLR.1-4. I.e. β˜ is estimated with a misspecifification as SLR.1 is assumed to be true.[4 marks]
(e)Under SLR.1-4, derive the probability limit of β˜.[4 marks]
(f)Additionally, suppose:
SLR.5 The error term u satisfifies V ar(u|x) =σ 2 for any value of x (homoskedasticity).
Under SLR.1-5, derive the (conditional) variance V ar(β˜|X).[4 marks]
Question 3 代写计量经济学作业
[22.33 marks]
(a)Answer the following questions.
(i)Consider the following regression models
M1 : yi = β0 + β1xi1 + β2xi2 + ui ,
M2 : yi = α0 + α1(xi1 − xi2) + ei .
Explain which model is more restrictive. Then explain how to test the restriction. Clearly state any assumptions you are making.[4 marks]
(ii) Consider the bivariate regression model
log y = β0 + β1 log x + u,
where y and x are measured in dollars. What will happen to the OLS intercept and slope estimates if we change the units of measurements from dollars to hundred dollars for both y and x?[3 marks] 代写计量经济学作业
(iii) Is the following statement true or false? Explain your answer.
Consider the multiple regression model yi = β0 + β1xi1 + β2xi2 + ui for i = 1, . . . , n. Let tβ1 and tβ2 be the t statistics for testing H0 : β1 = 0 and H0 : β2 = 0, respectively. If both tβ1 and tβ2 are zero, then the F statistic for the joint hypothesis H0 : β1 = β2 = 0 is also zero.[4 marks]
(b)In this question we will analyse a hypothetical sample of 1,387 UK-domiciled applicants who applied to study Economics at a UK university. We consider the following variables:
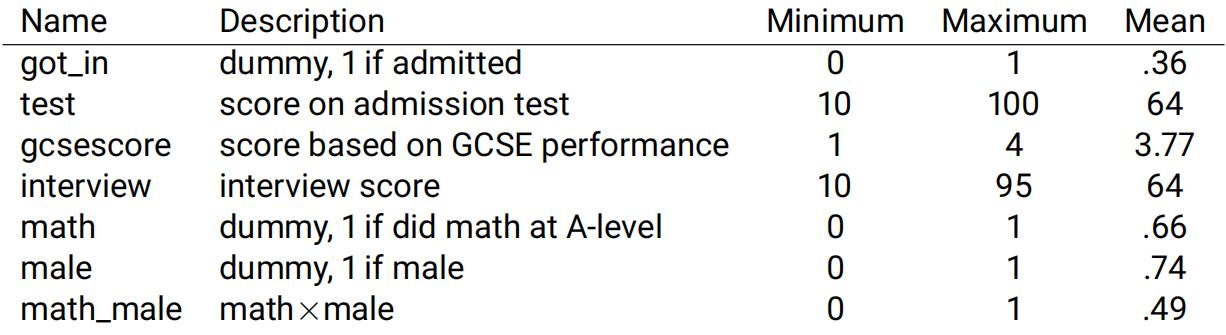
Using these data, a researcher estimates the following logit model for admission:
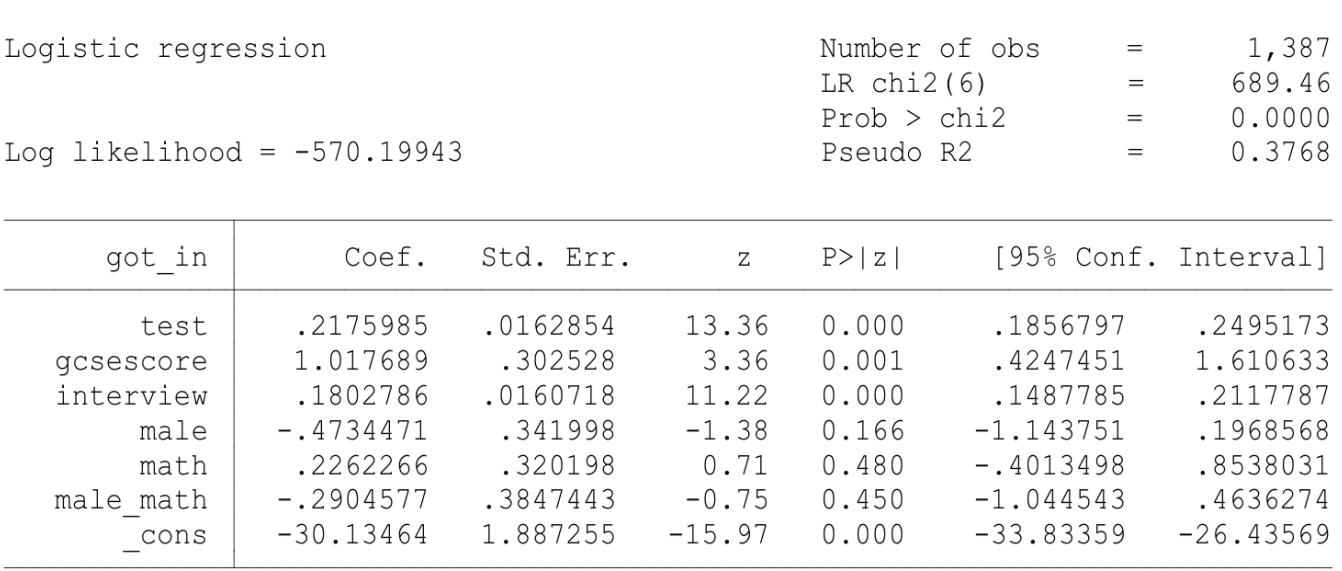
(i)Discuss clearly how the logit parameter estimates are obtained. You are expected to provde the log-likelihood function and will be rewarded for providing intuitions for the estimation procedure.[4.33 marks]
(ii) What is the difference in predicted probability of admission between a male and female student, who did math at A-level and scored the average mark in each assessment criterion? Interpret your fifinding.[4 marks]
(iii) How would you test if doing math at A-level inflfluences admission probability signifificantly?Clearly indicate your null and alternative hypothesis, the test statistic, its distribution under the null and the rejection rule.
Note: If you cannot conduct the test using the information provided, clearly indicate what additional information will be required to conduct the test.[3 marks]
Question 4 代写计量经济学作业
[22 marks]
It is postulated that more open economies have lower inflflation rates. A proposed model looks at a cross section of n countries using time averages:
inflfli = β0 + β1 log (inci) + β2 log (openi ) + ui ,i = 1, …, n. (4.1)
inflfli measures the average inflflation rate for country i, openi measures the openness of its economy (average share of imports in GDP), and inci its average per capita income. We can assume the errors do not exhibit autocorrelation.
(a)The model (4.1) was estimated by OLS and provided βˆ 2 = −.215 (with se(βˆ 2) = .095). If openness of the economy itself is also determined by the average inflflation rate (inflfli), what sort of problems will this cause for the OLS estimator for β2 in (4.1)? Explain.[3 marks]
(b)Suppose that, in addition to (4.1), the equation
openi = α0 + α1inflfli + α2 log (inci) + α3 log (landi) + vi (4.2)
holds, where landi is the land area of country i. Could this relation be helpful in providing a suitable method for estimating β2 in (4.1)? What would be the suitable estimation method and what conditions must be satisfified for it to be valid?[4 marks] 代写计量经济学作业
(c)Using the cross section of countries, the following regression was obtained by OLS:
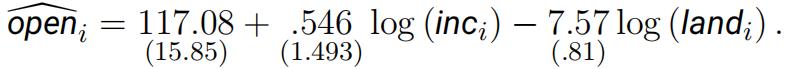
(4.3)
Robust standard errors are reported in parentheses. Discuss whether (and if so how) we can use this equation to verify whether the conditions in (b) are satisfified and discuss how this equation can help us to estimate β2. [4 marks]
(d)Explain the reason why robust standard errors were reported and how they would have been computed using (4.3).[3 marks]
(e)Discuss how you could have determined that robust standard errors were required in (4.3).[3 marks]
(f)Provide an intuitive explanation (use the method of moments framework) why you cannot provide an estimate for α1.[5 marks]

