Written assignment #3
数值分析书面作业代写 Consider the monomials: mk(x) = xk. (1) The monomials m0(x), m1(x), . . . , mn(x) form a basis for the set of degree n real polynomials:
Consider the monomials:
mk(x) = xk. (1)
The monomials m0(x), m1(x), . . . , mn(x) form a basis for the set of degree n real polynomials:
Pn = α0 + α1x + α2x2 + · · · + αnxn : (α0, . . . , αn) ∈ Rn+1 . (2)
Define an inner product on the set of square-integrable functions defined on [−1, 1] for a pair of functions f, g : [−1, 1] → R by:

Problem 2.
Plot p0, . . . , p5 on [−1, 1] using matplotlib and insert the plot inline in your submission using the LATEX graphicx package.
Problem 3. 数值分析书面作业代写
As we will see in the coming weeks, orthogonal polynomials are useful for approximating functions. Let f : [−1, 1] → R be square-integrable, and let p0, . . . , pn be a set of orthogonal polynomials on [−1, 1]. For a function g : [−1, 1] → R, define ∥g∥ by:
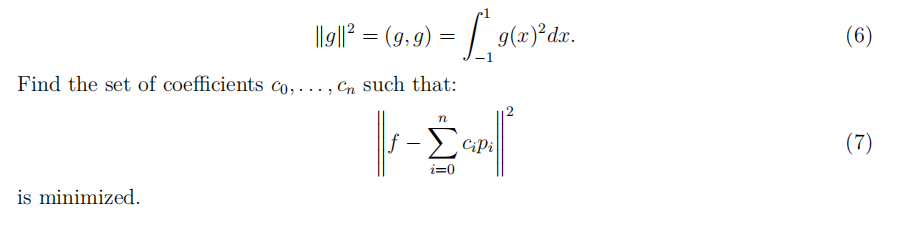
Problem 4. 数值分析书面作业代写
Pick three square-integrable functions defined on [−1, 1] which are not polynomials. They do not need to be smooth or even continuous. Now, for n = 5, compute the coefficients c0, . . . , c5 for each function f and form the approximation:

The relative error ekversus k, for k = 0, . . . , 5. Use a semilogy plot for this one.
You are free to do this problem by hand (except for the graphing, which must be done using Python), or you can do it using Python. If you use Python, please investigate using scipy.integrate.quadrature to compute the integrals—this will make your life easier.

更多代写:Web代写 GRE家考作弊 英国PSY网课代修 Problem solution essay代写 paper代写范文 新闻与传媒专业个人陈述范文代写
