ECE 6254 Spring 2019
Assigned April 22, 2019 – Revised April 22, 2019
加拿大数学代写 Giventwo points x1 and x2, show that ||x1− x2||22 can be computed using only linear com-binations of inner products.
Bonus Problem Set 4 加拿大数学代写
- This is an open book/Internet homework, but you should not interact with your classmates
- This is a bonus problem set with a single harddeadline
- Youwill receive a non-transferrable 2% bonus for using LATEX
- There are 2 problems over 3
- Theproblems are assigned the same weight for the overall
- Due Monday April 29, 2019 11:59pm EST (Monday May 6, 2019 for DistanceLearning Students)
- Pleaseturn in your solution using the LATEX template as the first page
Problem 1 加拿大数学代写
K-means clustering with the Euclidean distance inherently assumes that each pair of clusters is linearly separable, which may not be the case in practice. In this problem you will derive a strategyfor dealing with this limitation that we did not discuss in class. Specifically, you will show that like so many other algorithms we have discussed in class, K-means can be “kernelized.” In the following,we consider a dataset 
- Let
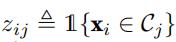, where Cj denotes the jth Show that the rule for updating thejth cluster center mj given this cluster assignment can be expressed as
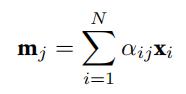
by expressing αij as a function of the zij’s.
- Giventwo points x1 and x2, show that ||x1− x2||22 can be computed using only linear com-binations of inner products.
- Giventhe results of the previous parts, show how to compute ||xi−mj||22 using only (linear combinations of ) inner products between the data points {xi}Ni=1.
- Describehow to use the results from the previous parts to “kernelize” the K-means clustering algorithm described in class.
Problem 2
In this problem we consider the scenario seen in class, where x is drawn uniformly on [−1, 1] and y = sin(πx), for which we are given N = 2 training samples. Here, we will consider an alternative approach to fitting a line to the data based on Tikhonov regularization. Specifically, we let
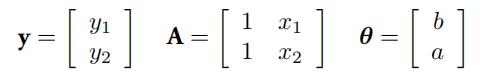
We will then consider Tikhonov regularized least squares estimators of the form
θˆ ≜ (A⊺A + Γ⊺Γ)−1A⊺y. (3) 加拿大数学代写
(a)Howshould we set Γ to reduce this estimator to fitting a constant function (i.e., finding an h(x) of the form h(x) = b)? (Hint: For the purposes of this problem, it is sufficient to set Γ in a way that just makes a 0. To make a = 0 exactly requires setting Γ in a way that makes the matrix A⊺A + Γ⊺Γ singular, but note that this does not mean that the regularized least-squares optimization problem cannot be solved; you must just use a different formula than the one in (3).
(b)Howshould we set Γ to reduce this estimator to fitting a line of the form h(x) = ax + b that passes through the observed data points (x1, y1) and (x2, y2)? 加拿大数学代写
(c)(Optional)Play around and see if you can find a (diagonal) matrix Γ that results in a smallerrisk than either of the two approaches we discussed in You will need to do this numeri- cally using Python or MATLAB. Report the Γ that gives you the best results. (You can restrict your search to diagonal Γ to simplify this.)
