CMP3751M Machine Learning
机器学习论文代写 There are 13 features in total: 4 sensors for each reading type, including power range, pressure and temperature.
Algorithms for Data Mining
Section 1: Data import, summary, preprocessing and visualization
Importing Data
The nuclear power plant data set is available in CSV format, which means that each value is separated by a comma, the feature header is defined on the first line, and then the data.
| Status |
| Power_range_sensor_1 |
| Power_range_sensor_2 |
| Power_range_sensor_3 |
| Power_range_sensor_4 |
| Pressure_sensor_1 |
| Pressure_sensor_2 |
| Pressure_sensor_3 |
| Pressure_sensor_4 |
| Temperature_sensor_1 |
| Temperature_sensor_2 |
| Temperature_sensor_3 |
| Temperature_sensor_4 |
By storing the data set in a data frame, can easily perform mathematical operations such as calculating the mean, standard deviation, minimum, and maximum.
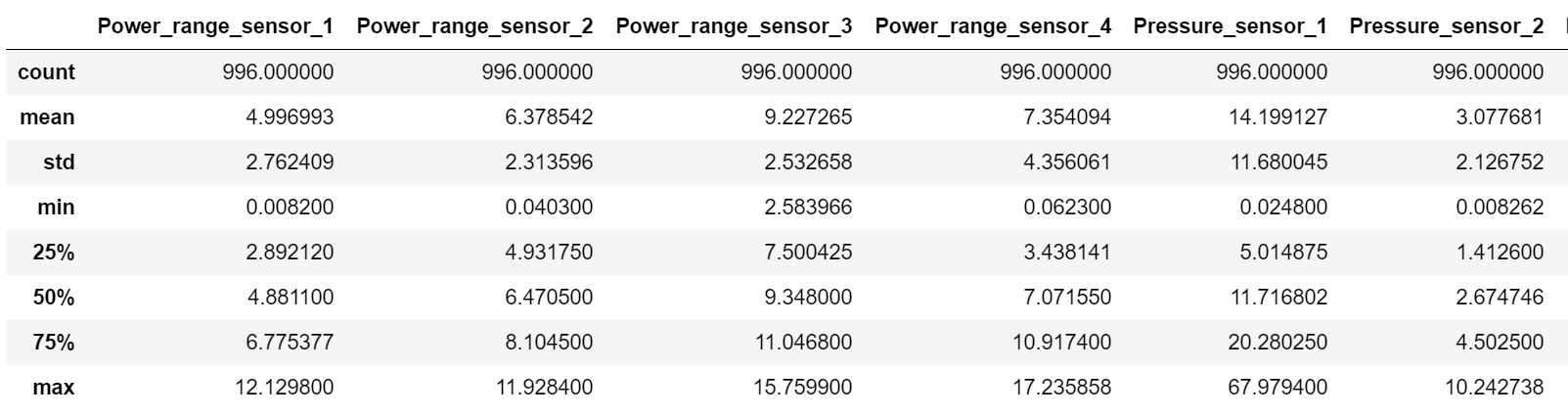
Data summary 机器学习论文代写
There are 13 features in total: 4 sensors for each reading type, including power range, pressure and temperature. The last feature contains categorical variables representing the state of the reactor, either “normal” or “abnormal”. There are no missing or null values in the data set.
———————————————————————————————————————-
Data Assignment2-dataset-nuclear_plants.csv
Features count:13
Records count:996
Feature Mean
Power_range_sensor_1 4.996993
Power_range_sensor_2 6.378542
Power_range_sensor_3 9.227265
Power_range_sensor_4 7.354094
Pressure _sensor_1 14.199127
Pressure _sensor_2 3.077681
Pressure _sensor_3 5.748279
Pressure _sensor_4 4.997002
Temperature_sensor_1 8.155479
Temperature_sensor_2 10.001593
Temperature_sensor_3 15.186910
Temperature_sensor_4 9.933125
dtype: float64
Pressure_sensor_1 is much larger than other pressure averages, and temperature_sensor_3 is also larger than other temperature values. This may indicate that there may be outliers in the data. However, this difference may be reasonable, as each sensor reads at a different location within the reactor.
Feature Std Dev
Power_range_sensor_1 2.762409
Power_range_sensor_2 2.313596
Power_range_sensor_3 2.532658
Power_range_sensor_4 4.356061
Pressure _sensor_1 11.680045
Pressure _sensor_2 2.126752
Pressure _sensor_3 2.526864
Pressure _sensor_4 4.165490
Temperature_sensor_1 6.174639
Temperature_sensor_2 7.336233
Temperature_sensor_3 12.159565
Temperature_sensor_4 7.282817
dtype: float64
The standard deviation of the pressure sensor 1 and the temperature sensor 3 is much larger than other sensors. This may indicate outliers in the data, but may be the result of different sensor positions.
Feature Min
Power_range_sensor_1 0.008200
Power_range_sensor_2 0.040300
Power_range_sensor_3 2.583966
Power_range_sensor_4 0.062300
Pressure _sensor_1 0.024800
Pressure _sensor_2 0.008262
Pressure _sensor_3 0.001224
Pressure _sensor_4 0.005800
Temperature_sensor_1 0.000000
Temperature_sensor_2 0.018500
Temperature_sensor_3 0.064600
Temperature_sensor_4 0.009200
dtype: float64 机器学习论文代写
Feature Max
Power_range_sensor_1 12.129800
Power_range_sensor_2 11.928400
Power_range_sensor_3 15.759900
Power_range_sensor_4 17.235858
Pressure _sensor_1 67.979400
Pressure _sensor_2 10.242738
Pressure _sensor_3 12.647500
Pressure _sensor_4 16.555620
Temperature_sensor_1 36.186438
Temperature_sensor_2 34.867600
Temperature_sensor_3 53.238400
Temperature_sensor_4 43.231400
dtype: float64
The max-min value of each function shows the highest data point read by each sensor. The maximum value of pressure sensor 1 is much higher than other pressure sensors, which again indicates that there may be abnormal values in the data.

Visualization
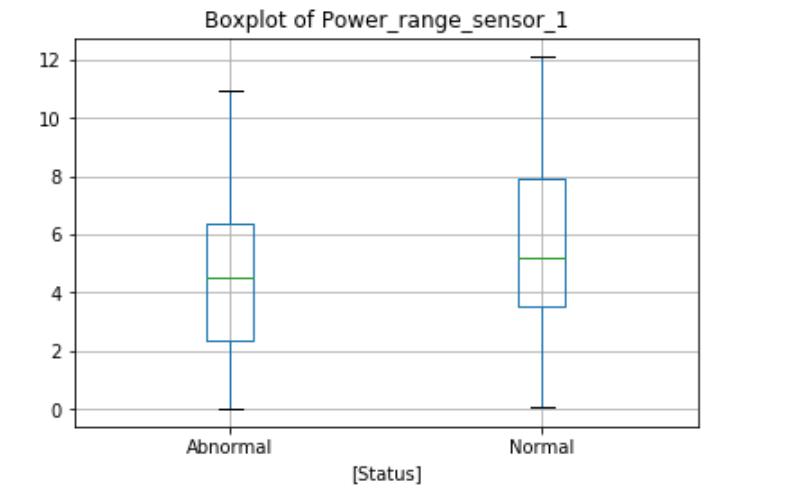
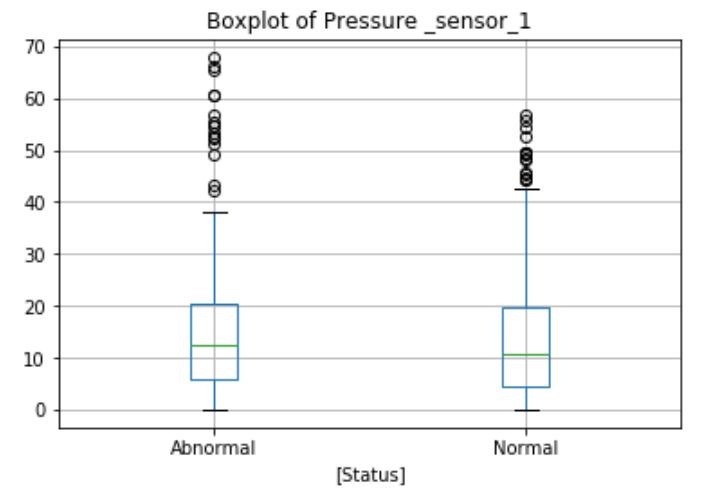
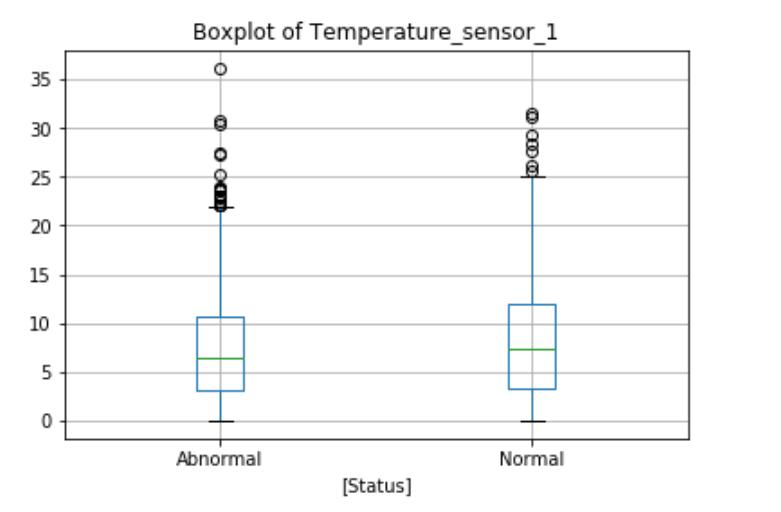
The Power_range_sensor_1 boxplot shows the differences in the normal and abnormal state categories. during normal operation, the average reactor power is slightly higher, and the maximum value and interquartile range are also higher. The boxplot will identify outliers above or below the maximum indicator for the circle, as shown here, there are no obvious outliers in this function. But the Temperature_sensor_1 and Pressure _sensor_1 boxplots show outliers exist in both data categories. These extremes may be measurement errors or natural outliers, which means that they are not errors but novelty in the data.
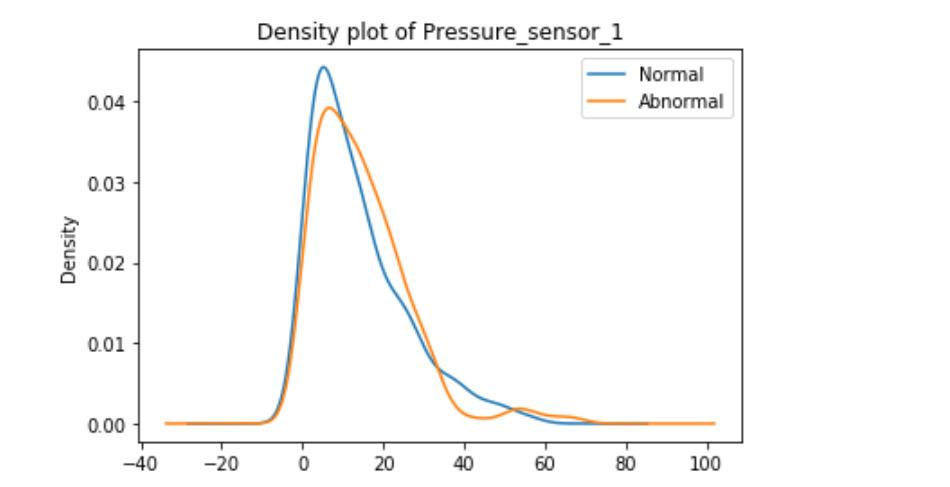
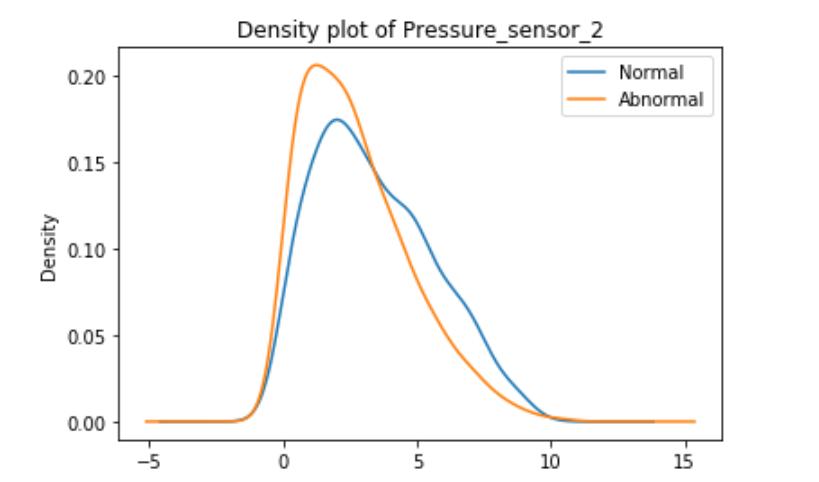
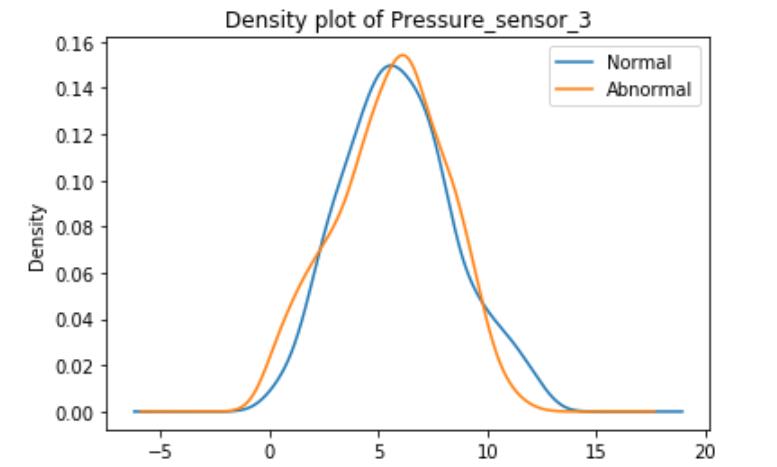
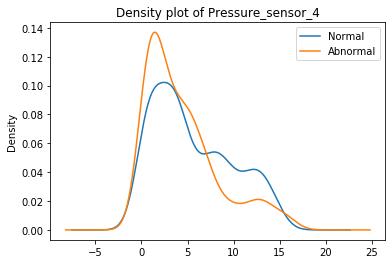
These graphs are density plots of the feature Pressure_sensor. The density plot visualizes the distribution of data through the continuous sensor values.
As suggested, there may be some underlying error or unexplained novelties within the data.
Preprocessing data
The data provided includes data from 3 different scales. Power, pressure and temperature are all measured using different indicators. Due to the deviation of one element from another in the network, differences in scale may lead to differences within the model. Therefore, before using the data in the ANN, the data must be normalized or standardized so that all functions reach the same scale.
Data standardization and standardization use the StandardScaler model and the standardized model in the Sklearn preprocessing sub-library.
They refer to the process of rescaling numeric attributes to the range of 0 and 1.
#——–Data Standardisation normalisation ———————
X = Data.drop(“Status”, axis=1)
scaler = StandardScaler()
X = scaler.fit_transform(X)
X = preprocessing.normalize(X, norm=’l2′)
Section 2: Selecting an algorithm
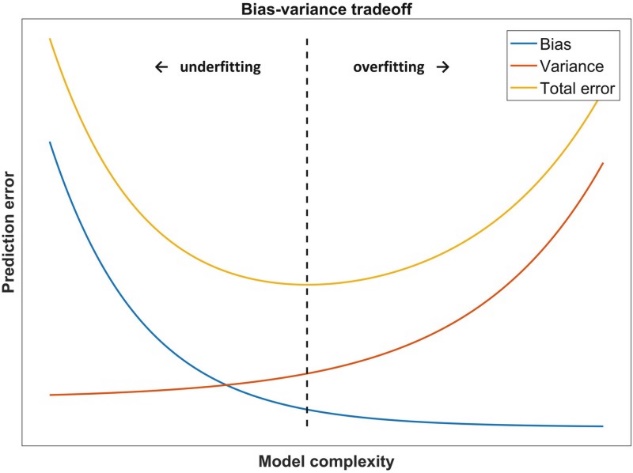
When designing a model, we often hope that the machine can learn a model with small empirical and generalization errors and which performs very well on both the training and test sets, but this is not the case in reality.
When the model complexity is higher, the degree of fit to the training set is higher, but the generalization ability of the new sample is reduced, and overfitting (overfitting) occurs at this time. 机器学习论文代写
In order to get a relatively stable model with good generalization ability, we should choose a model with appropriate complexity and good fit.
The complexity of the model gradually increases as the training of the sample progresses. At this time, the error on the training data set will gradually decrease. When the complexity of the model reaches a certain level, the error on the test set will increase with the complexity of the model Increase. It can be seen from the figure that the abscissa value of the red point is the model complexity we expect, and it performs well on both the training set and the test set.
In machine learning, all data is usually divided into three parts: training data set, validation data set, and test data set. Their functions are
Training dataset: used to build machine learning models
Validation dataset: assists in constructing the model, used to evaluate the model during the construction process, to provide an unbiased estimate for the model, and then to adjust the model’s hyperparameter
Test dataset: used to evaluate the performance of the trained final model
Constant use of test and validation sets will gradually make them ineffective. That is, the more times the same data is used to determine the hyperparameter settings or other model improvements, the lower the confidence that these results can be truly generalized to new data that has not been seen before. Note that the validation set usually fails more slowly than the test set. If possible, it is recommended to collect more data to “refresh” the test and validation sets. Restarting is a good way to reset.
Kuhn and Johnson point out in the “Data Splitting Recommendations” that using separate “test sets” (or validation sets) has certain limitations, including:
- The test set is a single evaluation of the model and cannot fully show the uncertainty of the evaluation results.
- Dividing a large test set into test and validation sets increases the bias of model performance evaluation. 机器学习论文代写
- The segmented test set sample size is too small.
- The model may require every possible data point to determine the model value.
- Different test sets generate different results, which results in great uncertainty in the test set.
- The resampling method can make a more reasonable prediction of the performance of the model on future samples.
Therefore, in practical applications, a K-fold cross-validation method can be selected to evaluate the model, which has low deviation and small changes in performance evaluation.
The K-fold cross validation method divides the data set into k mutually exclusive subsets of similar size, and tries to ensure the consistency of the data distribution of each subset. In this way, you can obtain k training-test sets for k trainings and tests.
k usually takes the value 10, which is called 10-fold cross validation. Other commonly used k values are 5, 20, and so on.
Section 3: Algorithm Design
Splitting data 机器学习论文代写
Data is split into a training set and a test set.
- training set—a subset to train a model.
- test set—a subset to test the trained model.

Ensure that the test set meets the following two conditions:
Large enough to produce statistically significant results.
Represents the entire data set. In other words, don’t choose a test set with different characteristics than the training set.
The train_test_split function is imported from the sklearn.model_selection sublibrary. test_size = 0.1 defines the size of the test set as 10% of the total dataset.
Model training
Multilayer Perceptron (MLP) is also called Artificial Neural Network (ANN). In addition to the input and output layers, it can have multiple hidden layers. The simplest MLP contains only one hidden layer, that is, three layers. The structure is as follows:
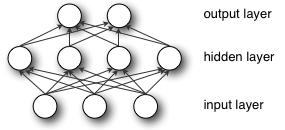
As can be seen from the above figure, the multilayer perceptron layers are fully connected to each other (fully connected means that any neuron in the previous layer is connected to all neurons in the next layer). The bottom layer of a multilayer perceptron is the input layer, the middle is the hidden layer, and the last is the output layer. 机器学习论文代写
To implement a multilayer perceptron classifier, use the MLPClassifier function in the sklearn.neural_network sub-library. This function creates a MLP algorithm model using backpropagation to reduce errors and generate a model that represents the input data. The function takes a number of parameters, including hidden_layer_sizes which defines the number of hidden layers and nodes in each layer.
After defining the model, you can fit it to the training data.
Random forest classifier 机器学习论文代写
In view of the shortcomings of decision trees that are easy to overfit, random forest uses a voting mechanism of multiple decision trees to improve the decision tree. We assume that random forest uses m decision trees. For a tree, it is obviously not desirable to train m decision trees with full samples. Full sample training ignores the law of local samples, which is harmful to the generalization ability of the model. The method of generating n samples uses Bootstrapping method. This is a sampling method with replacement, which produces n samples, and the final result is obtained using the Bagging strategy, that is, the majority voting mechanism.
To implement the random forest classifier, the RandomForestClassifier model function is imported from the sklearn.ensemble sub-library. n_estimators defines the number of trees in the forest, and min_samples_leaf defines the minimum number of samples required at the leaf nodes.
After defining the model, you can fit it to the training data.
result
| MLP Accuracy Score: 0.93 |
| Report: precision recall f1-score support |
| Abnormal 0.96 0.91 0.94 58 |
| Normal 0.89 0.95 0.92 42 |
| accuracy 0.93 100 |
| macro avg 0.93 0.93 0.93 100 |
| weighted avg 0.93 0.93 0.93 100 |
| 机器学习论文代写 |
| Tree Accuracy Score : 0.96 |
| Report: precision recall f1-score support |
| Abnormal 0.97 0.97 0.97 58 |
| Normal 0.95 0.95 0.95 42 |
| accuracy 0.96 100 |
| macro avg 0.96 0.96 0.96 100 |
| weighted avg 0.96 0.96 0.96 100 |
This table shows the results of the test set accuracy results.
Section 4: Model Selection
K-fold cross validation:
sklearn.model_selection.KFold (n_splits = 10, shuffle = False, random_state = None)
Idea: Divide the training / test data set into n_splits mutually exclusive subsets, use one of them as the validation set at a time, and use the remaining n_splits-1 as the training set. Perform n_splits training and testing to get n_splits.
———————————————————————————————————————-
model_MLP = MLPClassifier()
parameters = {‘hidden_layer_sizes’:[25,100,500]}
gridsearch = GridSearchCV(model_MLP, parameters, cv=10, iid=False, return_train_score=True)
gridsearch.fit(x_train,y_train)
print(gridsearch.cv_results_[‘mean_test_score’])
print(gridsearch.best_estimator_)
[0.80475861 0.85952957 0.8929647 ] 机器学习论文代写MLPClassifier(activation=’relu’, alpha=0.0001, batch_size=’auto’, beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=500, learning_rate=’constant’,
learning_rate_init=0.001, max_iter=200, momentum=0.9,
n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,
random_state=None, shuffle=True, solver=’adam’, tol=0.0001,
validation_fraction=0.1, verbose=False, warm_start=False)
model_RF = RandomForestClassifier()
parameters = {‘n_estimators’:[10,50,100]}
gridsearch = GridSearchCV(model_RF, parameters, cv=10, iid=False, return_train_score=True)
gridsearch.fit(x_train,y_train)
print(gridsearch.cv_results_[‘mean_test_score’])
print(gridsearch.best_estimator_)
[0.89835961 0.91746018 0.91965826]RandomForestClassifier(bootstrap=True, class_weight=None, criterion=’gini’,
max_depth=None, max_features=’auto’, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
———————————————————————————————————————-
Conclusion 机器学习论文代写
After training a supervised learning algorithm in the form of a multilayer perceptron and a random forest classifier, the random forest model performs more robust and excellent.
Neural networks often require large numbers, and random forest models on small data sets have obvious advantages. Neural networks often require more demanding data preparation, and random forest models generally do not require data processing. And the difficulty of tuning the random forest model is much lower than the neural network. And the interpretation of integrated tree models is generally higher.
Generally speaking, with a small amount of data and many features, integrated tree models are often better than neural networks.
References
Gardner M W, Dorling S R. Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences[J]. Atmospheric environment, 1998, 32(14-15): 2627-2636.
Pal M. Random forest classifier for remote sensing classification[J]. International Journal of Remote Sensing, 2005, 26(1): 217-222.
Kriegel H P, Kröger P, Zimek A. Outlier detection techniques[J]. Tutorial at KDD, 2010, 10. 机器学习论文代写
Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Ijcai. 1995, 14(2): 1137-1145.
Claeskens G, Hjort N L. Model selection and model averaging[R]. Cambridge University Press, 2008.
Anderson D, Burnham K. Model selection and multi-model inference[J]. Second. NY: Springer-Verlag, 2004, 63.

更多代写:澳大利亚网课托管价格 网上代考 澳洲代写assignment 澳洲哲学代上网课 北美Finance代写 博士论文怎么写能够合格
