MATH 3510 HOMEWORK 9
数学编程作业代写 Instructions: For written questions, write your answers on your own papers. For programming questions, submit your codes using MATLAB Grader.
Instructions: For written questions, write your answers on your own papers. For programming questions, submit your codes using MATLAB Grader.
1.(Numerical Differentiation) 数学编程作业代写
Recall that we derived in class a numerical differentiation formula
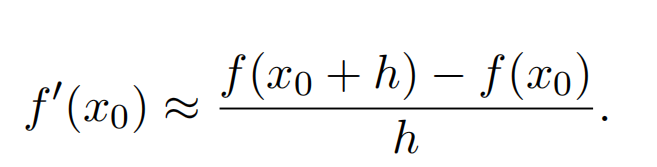
We call this formula forward-difference formula if h > 0 and backward-difference formula if h < 0. Use the forward-difference formula and backward-difference formula to determine each missing entry in the following tables. You must show your work. You can simply compute these by hand.
| x | f(x) | F’(x) |
| 0.5 | 0.4794 | |
| 0.6 | 0.5646 | |
| 0.7 | 0.6442 |
2.(Forward Euler’s Method) 数学编程作业代写
Implement Euler’s method in MATLAB. See detailed instructions in MATLAB Grader. Use your code to solve the following initial-value problem,


Remark. You need to include the codes you use for part [a.], [b.] and [c.] in MATLAB Grader. You also need to report the results in the written part.
3.(Runge-Kutta Method)
Recall that RK4 method is a one-step multistage method to solve the following initial value problem,
y’ = f(t, y(t)), t ∈ [a, b], y(a) = α.
The scheme is
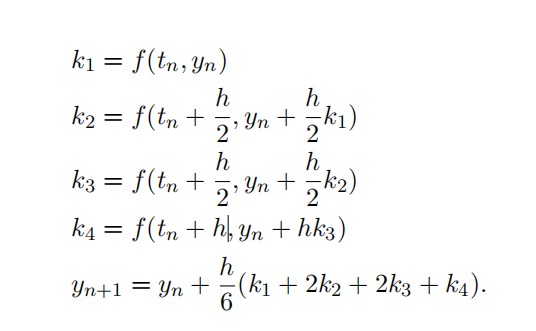
a. Implement the RK4 method we introduced in class. See detailed instruction in MATLAB Grader.
b. Note that RK4 method requires four function evaluations per step while Euler’s method requires only one function evaluation. Hence four steps of Euler’s method and one step of RK4 method have the same number of function evaluations. With the same function evaluations, we expect RK4 outperforms Euler’s method since RK4 is an O(h4) method and Euler’s method is an O(h) method. We verify this obeservation by the following numerical experiment.
Solve the following equation
Y’ = te3t − 2y, 0 ≤ t ≤ 1, y(0) = 0.
by Euler’s method with h = 0.025 and RK4 method with h = 0.1 (using your MATLAB codes). Compare the results by two methods at t = 0.1, 0.2, 0.3, 0.4 and 0.5. Complete the following table.
| t | Exact | Euler with h = 0.025 | RK4 with h = 0.1 |
| 0.0 | 0 | 0 | 0 |
| 0.1 | 0.0058 | ||
| 0.2 | 0.0268 | ||
| 0.3 | 0.0711 | ||
| 0.4 | 0.1508 | ||
| 0.5 | 0.2836 |

更多代写:美国Python网课代上 线上考试 英国数学代上网课 PPT内容模板代写 conclusion代写 summary写作代写
