SUMMER TERM 2016 ECON3014: GAME THEORY
TIME ALLOWANCE: 2 hours
代考博弈论 The second oldest son, decides which of the two plots goes to the oldest son and divides the other plot into two plots.
Answer any THREE questions. All questions carry equal weight.
In cases where a student answers more questions than requested by the examination rubric, the policy of the Economics Department is that the student’s first set of answers up to the required number will be the ones that count (not the best answers). All remaining answers will be ignored.
1.A rich landlord unexpectedly passes away and leaves a homogeneous plot of land as an inheritance to his n The sons use the following way to divide the land betweenthemselves.
They take actions sequentially according to seniority starting with the oldest. The oldest son divides the land into two plots (he is free to choose the relative sizes of these plots).
The second oldest son, decides which of the two plots goes to the oldest son and divides the other plot into two plots. The third son decides which of the latter two plots goes to the second oldest son and divides the other plot into two plots. This goes on until the youngest son gets to act. Since he is the last one, he just decides which of the two offered plots he takes for himself and which goes to his brother who acted before him. All n brothers want to get as much land as they can. 代考博弈论
(a)Assume that n = 2. Formalize this situation as a game. Which equilibrium conceptis the most appropriate? Find an equilibrium and discuss its unique- ness.
(b)Assume that n = 3. Find an equilibrium.
(c)Find an equilibrium for any n > What is the size of the plot of land that thekth oldest son gets in equilibrium?

2.Consider the following hide-and-seek game between two Player 1 puts a dollar bill into one of the three boxes without telling Player 2. 代考博弈论
Player 2 picks one box of his choice and opens it. Player 2 gets to keep the content of the box he openedand the content of the other two boxes remains with Player 1.
(a)Formulatethis as a game in an extensive Argue that there is no equilibria in pure strategies.
(b)Solve for an equilibrium. 代考博弈论
(c)Considerthe following modification of the At the beginning of the game Player 1 puts a dollar into a box of his choice without telling Player 2 the location of the dollar. Player 2 then takes one box, but does not open it yet. After that, Player 1 has to choose one of the two remaining boxes and show its content to Player 2.
Once it is done, Player 2 can either keep the box that he previously selected or can reconsider and take one of the two other boxes. Once Player 2 makes his final choice, the game ends. At the end of the game Player 2 gets the content of the box he obtained and the content of the other two boxes remains with Player 1. Solve for an equilibrium of the game. Does Player 2 always open the box he has originally chosen or does he reconsider? Give an intuition for your answer.
3.Consider a homogenous good market with two The demand for a good is Q = A -p where p is the price and A > 0 is a parameter.
Both firms can produce thegood at no cost. Firm 1 maximizes its profits and firm 2 is unconcerned about its profits. Instead, firm 2 maximizes the following utility function
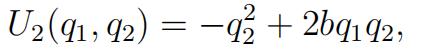
where qi is the production of firm i and b > 0 is a parameter.
(a)Solvefor a pure strategy Nash equilibrium of the game where two firms choose their quantities simultaneously. 代考博弈论
(b)Solve for a subgame perfect Nash equilibrium of the game in which firm 1 chooses its quantity first and firm 2 chooses its quantity after observing the choice of firm 1.
(c)Solve for a subgame perfect Nash equilibrium of the game in which firm 2 chooses its quantity first and firm 1 chooses its quantity after observing the choice of firm 2.
4.Considerthe following model of presidential There are three candidates. 代考博弈论
Each candidate can be either good or bad. The type of a candidate is drawn at random in the beginning of the game. The probability of drawing a good type is π. The type is a private information of a candidate.
There are two periods in this model. In the first period, the first two candidates participate in the election (the third candidate remains idle) and the candidate that wins becomes a president in the first period. The president’s type is revealed to the public.
In the second period, the incumbent participates in the election against the third candidate, and the person that wins becomes a president in the second period. Each candidate is risk-neutral and values the office at v (this value is per term).
In the first period, the candidates can finance their political campaigns using their own funds. The amount e spent on the campaign is publicly observable. You can assume that the candidates have quasilinear utility (and no budget constraints): each candidate maximizes 代考博弈论
E[k]v − e,
where E[k] is the expected number of periods the candidate occupies the office.
Both candidates have to make their campaign finance decisions simultaneously and independently of each other. (Hint: the monies spent on the political campaign do not affect the quality of the candidates but they may affect the voters’ perception of the candidates’ quality)
The voters are all identical. They prefer a good candidate over a candidate of unknown quality and they also prefer a candidate of unknown quality over a bad one. You can assume that if the voters are indifferent, they elect either candidate with probability 1/2.
(a)Find an equilibrium in which candidates do not spend any money on their campaign.
(b)Find an equilibrium in which some candidates spend money on their campaign.
(c)Aparliament introduces a law that imposes an upper limit on the amount of money that a candidate can spend on his campaign. How does such a law affect the equilibrium payoffs of the candidates and the welfare of the voters?

更多代写:新加坡代写作业 托福网考作弊 新西兰代写assignment 医学代写 艺术Assignment代做 case study怎么写
