MATH2720 Multi-variable Calculus: Assignment 4
代写多变量微积分作业 You must submit your signed Academic Integrity Declaration form and completed problem set on Crowdmark by the deadline.
CrowdMark Instruction
We will be using Crowdmark to grade assignment/test submissions. You will get a personalized submission link sent to your UManitoba email address. Do NOT share this link with other students.
If you cannot find the notification email in your inbox, check your spam folder or search your email for all emails containing the word ”crowdmark.”
If you really cannot find your link, contact Dr. Xinli ([email protected]) at least a day before the assignment deadline, and I will re-send it to you. Make sure you use the email policy so your email is not filtered out.
How do I write my solutions? 代写多变量微积分作业
- Option 1: Write your answers electronically. Convert your solutions to pdf when you are done, such that each question starts in a new file.
- Option 2: Write your answers by hand. Then take a picture with your phone (not recommended) or scan your answers (using the library scanners, or a mobile app like Scanbot or Microsoft Office Lens or Google Drive (Android only)(recommended). Make sure each question starts in a new file, and that your picture/scan is clear and legible. You will receive no credit if your answers cannot be clearly read.
How do I submit my work? 代写多变量微积分作业
- Click the link in your notification email from Crowdmark.
- Upload your answers to each question separately. (You may use multiple pages perquestion)
- Rotatepages if necessary, and order pages correctly for each question.
- Submit.
- Save a copy of the confirmation page for your records.
- You are allowed to change your answers by resubmitting as many times as you need before the deadline.
Submission of Assignment
You must submit your signed Academic Integrity Declaration form and completed problem set on Crowdmark by the deadline.
- Late assignments will not be accepted.
- Consider submitting your assignment well before the deadline.
- If you require additional space, please insert extra pages.
- You must justify and support your solution to each question.

Academic Integrity Declaration 代写多变量微积分作业
Declaration: I, the undersigned, declare that all the work I will submit to fulfill the requirements for this assessment is wholly my own work. During the test/exam I will not:
- copy by manual or electronic means from any work produced by any other person or persons, present or past, including tutors or tutoringservices;
- share questions or answers in whole or in part with anyone, including posting portions of the test/exam in publicly accessiblelocations;
- copy from any source including textbooks and websites,or
- consultexternal websites, online forums, search engines, or any resource not appearing in the list of acceptable test materials above. 代写多变量微积分作业
Students must not discuss or communicate the contents of the test or exam with any person except their instructor until 24 hours after the end of the test or exam.
By signing this document, I acknowledge that I have read and will follow the instructions for acceptable material during the test/exam.
I understand that penalties for submitting work which is not wholly my own, or distributing my work to other students, isconsidered an act of Academic Dishonesty and is subject to penalty as described by the University of Manitoba’s Student Discipline Bylaw. These penalties that may apply range from a grade of zero for work, failure in the course, to expulsion from the University.
Name:
Student number:
Date:
Signature:
List of problems 代写多变量微积分作业
| D\L | −80 | −70 | −60 | −50 | −40 | −30 | −20 | −10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 1 | 1440 | 1440 | 1122 | 977 | 897 | 843 | 799 | 762 | 727 | 693 | 657 | 615 | 563 | 489 | 362 | 0 | 0 |
| 32 | 1440 | 1225 | 995 | 904 | 850 | 811 | 779 | 753 | 727 | 702 | 676 | 646 | 610 | 559 | 478 | 292 | 0 |
| 60 | 1183 | 914 | 841 | 804 | 780 | 763 | 749 | 737 | 727 | 715 | 705 | 692 | 677 | 656 | 626 | 567 | 378 |
| 91 | 551 | 640 | 671 | 687 | 699 | 707 | 714 | 720 | 726 | 733 | 740 | 748 | 759 | 773 | 796 | 839 | 975 |
| 121 | 208 | 549 | 514 | 582 | 625 | 656 | 682 | 706 | 727 | 749 | 772 | 799 | 833 | 881 | 958 | 1131 | 1440 |
| 152 | 0 | 0 | 383 | 502 | 571 | 621 | 660 | 695 | 727 | 760 | 796 | 836 | 888 | 964 | 1097 | 1440 | 1440 |
| 172 | 0 | 0 | 352 | 484 | 559 | 613 | 655 | 698 | 727 | 763 | 801 | 845 | 901 | 982 | 1132 | 1440 | 1440 |
| 182 | 0 | 0 | 360 | 488 | 562 | 614 | 654 | 693 | 727 | 762 | 799 | 843 | 898 | 978 | 1123 | 1440 | 1440 |
| 213 | 0 | 253 | 461 | 549 | 603 | 641 | 673 | 701 | 727 | 753 | 782 | 815 | 856 | 915 | 1013 | 1281 | 1440 |
| 244 | 333 | 550 | 616 | 649 | 672 | 689 | 702 | 715 | 726 | 738 | 752 | 766 | 785 | 811 | 851 | 932 | 1252 |
| 274 | 904 | 808 | 777 | 760 | 750 | 742 | 736 | 731 | 726 | 722 | 718 | 713 | 707 | 701 | 690 | 671 | 616 |
| 305 | 1440 | 1107 | 947 | 874 | 828 | 796 | 770 | 758 | 727 | 707 | 685 | 660 | 630 | 589 | 524 | 390 | 0 |
| 335 | 1440 | 1440 | 1091 | 960 | 887 | 836 | 794 | 760 | 728 | 695 | 661 | 622 | 573 | 505 | 389 | 0 | 0 |
| 356 | 1440 | 1440 | 1133 | 983 | 901 | 845 | 801 | 763 | 728 | 693 | 655 | 613 | 559 | 485 | 353 | 0 | 0 |
Table 1: Number of minutes of sunlight.
1.Table 1 shows M (D, L), the number of minutes of sunlight per day as a function of the day D of the year and latitude L. 代写多变量微积分作业
Positive latitudes indicate degrees north of the equator, negative latitudes indicate degrees south of the equator. (Note: Grand Rapids is at approximately 43◦ latitude.)
(a)Estimate as best you can each of the first order partial derivatives and write one sentence that describes, in context, the meaning of the derivative. Include appropriate units in your description.
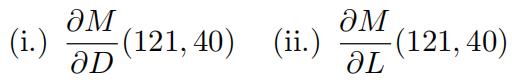
(b)Estimate as best you can each of the second order partial derivatives and write one sentence thatdescribes, in context, the meaning of each. Include appropriate units in your description. Carry your approximations to two decimal places. Is Clairaut’s Theorem satisfied? Explain. 代写多变量微积分作业
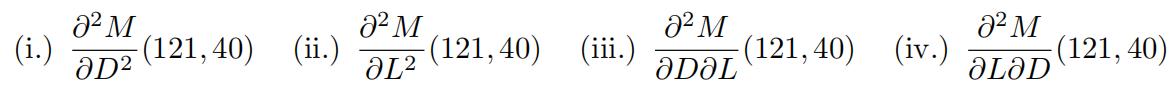
2.Findthe limit, if it exists, or demonstrate that the limit does not exist.
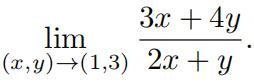
(a)
(b)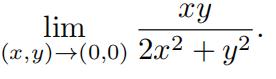
3.Find all first and second order partial derivatives.
(a)f(x, y) = y2 − cos(xy)
(b)![]()

