Math 541
HW4 – Dual Space, Determinant, Rotations
代写数学课业 Remarks: A) Definition is just a definition, there is no need to justify or explain it. B) Answers to questions with proofs should be
Remarks: 代写数学课业
A) Definition is just a definition, there is no need to justify or explain it.
B) Answers to questions with proofs should be written in the followingformat:
i) Statement and/or Result.
ii) Main points that will appear in your proof.
iii) The actual proof.
C) Answers to questions with computations should be written in thefollowing format:
i) Statement and/or Result.
ii) Main points that will appear in your computation.
iii) The actual computation.
1. 代写数学课业
Dual space. Let V be a finite dimensional vector space over a field F.
The dual space of V , denote V* , is defined to be the space
V* = Hom(V, F) = {φ : V → F; φ is linear transformationg},
of all linear transformations from V to F. The elements of V* are, sometime, called functionals.
(a) Show that dim(V ) = dim(V* ).
(b) Suppose now that F = R, and V is an inner product space, with inner product ( , ). Consider the natural mapping


3. 代写数学课业
The orthogonal group O2. We know that
O2 ={A ∊GL2; AAt = I2}: (2)
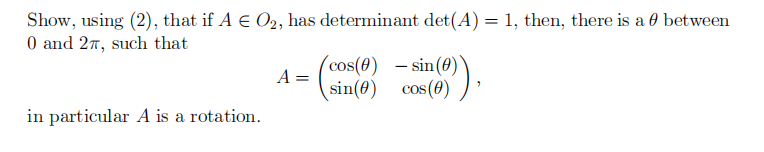
- You are welcome to consult the lecturer on HW during office hours.
- You are very much encouraged to work with other students on the HW.
- You should submit your HW ALONE in YOUR OWN ORIGINAL DOCUMENT!!!
Good Luck!

