Math 2415 Midterm 1
代考数学考试 The problems must be solved without any assistance of others or the usage of unauthorized material or information.
To get full credit you must show ALL your work.
The problems must be solved without any assistance of others or the usage of unauthorized material or information. This is a “closed book” exam: no texts, notes or calculators allowed.

2.(20 points) 代考数学考试
Water flows into and out of a reservoir with volume V at a constant rate of . The reservoir initially contains pure water, but then the water coming in has a concentration of of a certain pollutant. The reservoir is well-stirred so that the concentration of pollutant in it is uniform at all times.
Let denote the quantity of pollutant in the water at time
Let denote the concentration of pollutant in the water at time
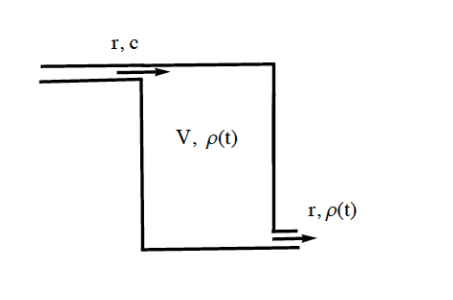
(a) Find an expression for the change in the quantity of pollutant during the time interval Δ, that is, find 𝑄(𝑡 + ∆𝑡) − 𝑄(𝑡).
(b) Now, find an expression for 𝜌(𝑡 + Δ𝑡) − 𝜌(𝑡)
(c) Compute the limit as Δ𝑡 → 0 of the expression that you found on part (b)
(d) Your result from part (c) is a differential equation, write it in standard form, specify units and state the initial condition.
DO NOT SOLVE THE DIFFERENTIAL EQUATION THAT YOU FIND.
3.(20 points) 代考数学考试
An electric circuit with a capacitor C, an inductor L and a resistor R. No external voltage is applied. The equation for the charge Q(t) on the capacitor is:
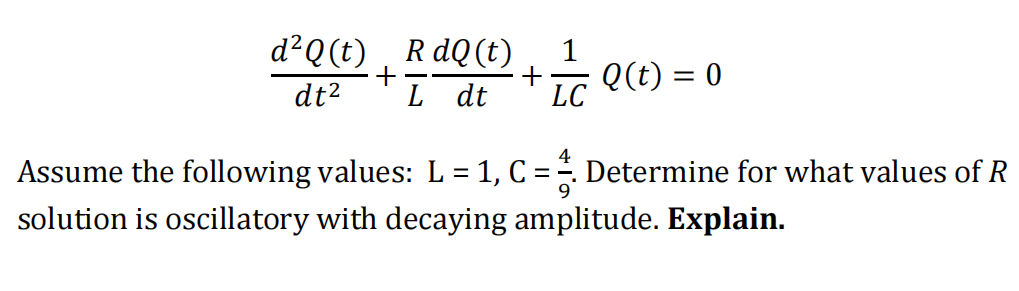
4.(20 points)
Suppose that 𝑦1(𝑡) = 𝑒−3 , 𝑦2(𝑡) = 𝑡𝑒−3t are solutions to the differential equation
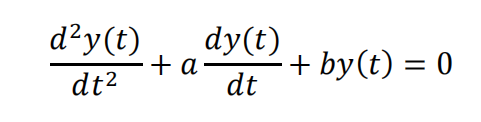
(a) Show that Wronskian of the solutions 𝑦1(𝑡) and 𝑦2(𝑡) is not zero for all .
(b) General solution to the differential equation
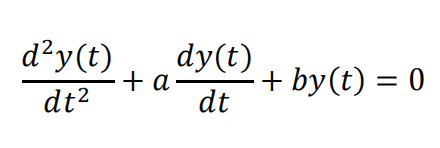
is 𝑦(𝑡) = (𝐶1 + 𝐶2𝑡)e−3t, where 1 and 2 are arbitrary real numbers. Find a,b .

更多代写:留学生CS网课代包 ap代考 英国留学生社会学assignment代写 留学生论文代写推荐 留学生申请文书写作 代写硕士毕业论文价格
